
非线性物理:混沌物理 受驱Benard,对流实验: ·通过同步与锁模走向混沌的例子有许多,鉴于实际测量的复杂性 ,完美显示混沌进程需要精细设计与巧妙技术。 以实验首次证明倍周期分岔闻名的利布沙伯技高一筹。他们采用 水银来做对流实验,水银是导体,可以加入电流驱动第二振子。 实验结果清晰地给出了振荡锁模的阿诺德舌头,以及进入混沌的 准周期道路。 下面看看实验结果:
非线性物理:混沌物理 受驱Benard对流实验: • 通过同步与锁模走向混沌的例子有许多,鉴于实际测量的复杂性 ,完美显示混沌进程需要精细设计与巧妙技术。 • 以实验首次证明倍周期分岔闻名的利布沙伯技高一筹。他们采用 水银来做对流实验,水银是导体,可以加入电流驱动第二振子。 • 实验结果清晰地给出了振荡锁模的阿诺德舌头,以及进入混沌的 准周期道路。 • 下面看看实验结果:
非线性物理:混沌物理 s c 明显的锁模行为发生在激励 12 1 29 34 需 需 电流升高的过程中。 201 混沌临界点不是水平线。 (毫安) 0G=[1,1,1,小 10 1 子 子 1+ 3 1 + 1+ V5-1 0 s =0.618033985 0.3 0.5 0.7 0.9 2 频率比D80/0ExT R=4.09R 0s=[2,2,2,]=V√2-1=
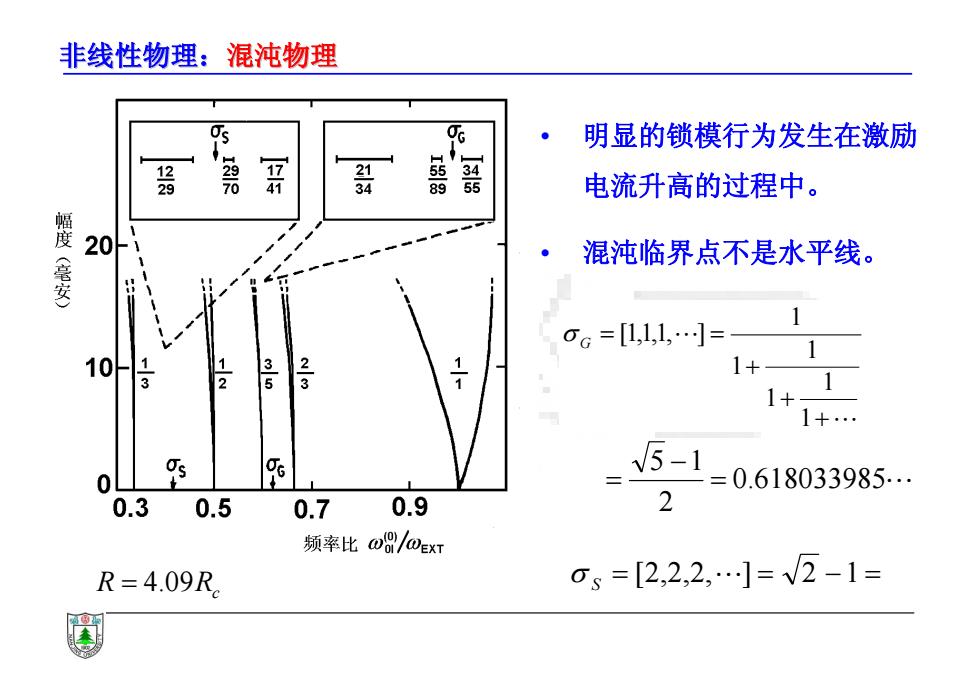
非线性物理:混沌物理 • 明显的锁模行为发生在激励 电流升高的过程中。 • 混沌临界点不是水平线。 1 1 1 1 1 1 [1,1,1, ] G 0.618033985 2 5 1 S [2,2,2,] 2 1 R Rc 4.09
非线性物理:混沌物理 (db) 当驱动电流低于临界电流时,信号的功 -20 率谱主要由两个基频线性组合得到的少 (a) 数谱峰;当达到临界驱动电流时,组合 得谱峰数便很快增加起来,尤其是低频 (b 分量的密度越来越多;而当超过临界电 流时,高频逐步地为噪声所替代,这是 进入了混沌的特征。 (c) (a)为16.9mA,低于临界电流;(b)为 80 17.4mA,最接近临界电流;(c)为 0.5 频率(Hz) 21.5mA,高于临界电流
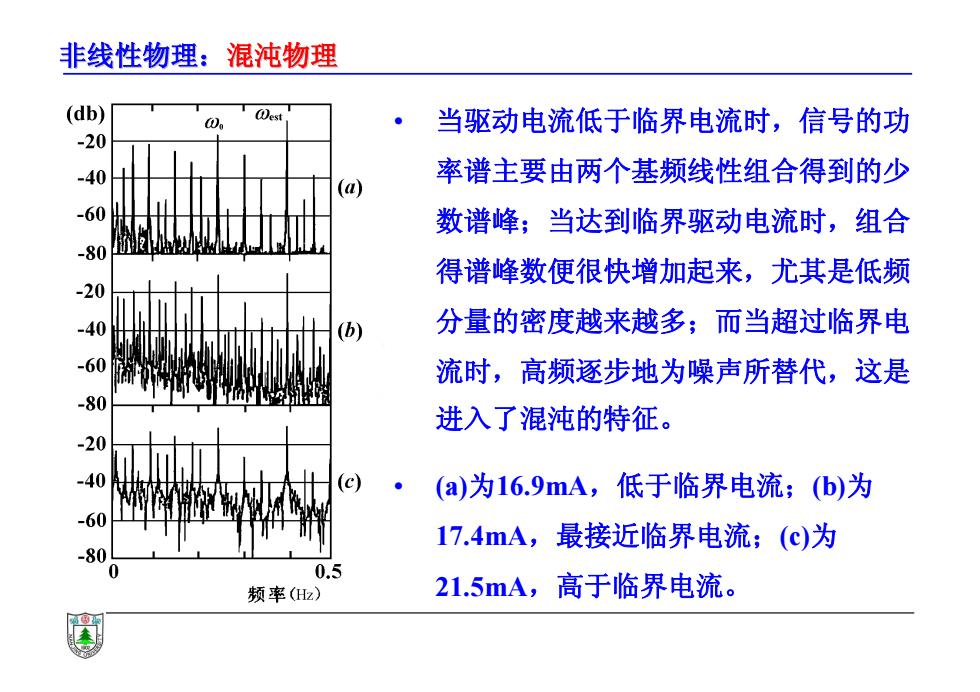
非线性物理:混沌物理 • 当驱动电流低于临界电流时,信号的功 率谱主要由两个基频线性组合得到的少 数谱峰;当达到临界驱动电流时,组合 得谱峰数便很快增加起来,尤其是低频 分量的密度越来越多;而当超过临界电 流时,高频逐步地为噪声所替代,这是 进入了混沌的特征。 • (a)为16.9mA,低于临界电流;(b)为 17.4mA,最接近临界电流;(c)为 21.5mA,高于临界电流

非线性物理:混沌物理 电子混沌电路: 采用电子电路容易实现各类非线性动力学体系,且电子测量比其 它物理量测量更为方便,如果采用示波器可以直接获得被测量数 据的图形,如果将数据采用计算机处理,可以计算出各类非线性 动力学参数。 因此电子混沌电路在混沌研究中占有重要地位。 电子混沌电路基本上可以分成三类:一是外激励的非线性LC谐振 电路;二类是模拟微分方程的电子电路;三是实际动力体系的电 子模拟电路
非线性物理:混沌物理 电子混沌电路: • 采用电子电路容易实现各类非线性动力学体系,且电子测量比其 它物理量测量更为方便,如果采用示波器可以直接获得被测量数 据的图形,如果将数据采用计算机处理,可以计算出各类非线性 动力学参数。 • 因此电子混沌电路在混沌研究中占有重要地位。 • 电子混沌电路基本上可以分成三类:一是外激励的非线性LC谐振 电路;二类是模拟微分方程的电子电路;三是实际动力体系的电 子模拟电路
非线性物理:混沌物理 非线性缸C谐振电路: ·外激励的非线性LC谐振电路中,通常使用一些非线性电子元件, 即非线性电阻、非线性电容、非线性电感等。考虑单结晶体管混 沌电路。 ·在使用单结晶体管作为非线性电阻时,电路示意图很简单: m 40c0s(2x) R1
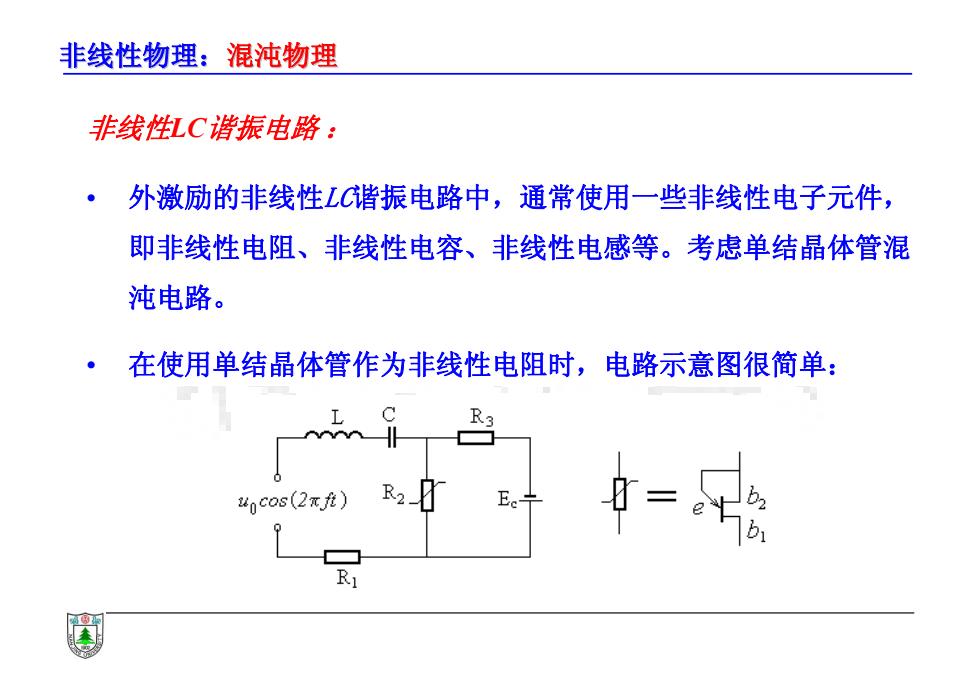
非线性物理:混沌物理 非线性LC谐振电路 : • 外激励的非线性LC谐振电路中,通常使用一些非线性电子元件, 即非线性电阻、非线性电容、非线性电感等。考虑单结晶体管混 沌电路。 • 在使用单结晶体管作为非线性电阻时,电路示意图很简单: