
非线性物理:混沌物理 混沌的几何特征: 通过前面的一系列具体实例、李雅普洛夫指数和吸引子形态的分 析,我们明白非线性系统的演化来自于驱动、耗散和非线性的共 同作用。 ·驱动使系统离开原来状态,耗散保持系统整体结构,非线性使系 统具有几何与拓扑上的多样性。 ·从几何学上理解混沌结构是有价值的。 从简单例子开始:
非线性物理:混沌物理 混沌的几何特征: • 通过前面的一系列具体实例、李雅普洛夫指数和吸引子形态的分 析,我们明白非线性系统的演化来自于驱动、耗散和非线性的共 同作用。 • 驱动使系统离开原来状态,耗散保持系统整体结构,非线性使系 统具有几何与拓扑上的多样性。 • 从几何学上理解混沌结构是有价值的。 • 从简单例子开始:

非线性物理:混沌物理 2xn,0≤xn≤1/2 帐篷映射:Xn+1=T(xn)= 2-2xn,1/2<xn≤1 2xn,0≤xn<1/2 锯齿映:Xn+1=S(Xn)= 2xn-1,1/2≤xn≤1 这两类映射具有局域演变的两个特点:伸长与折叠。 帐篷映射第一半是驱动过程,具有伸长性质;后一半是耗散反馈 过程,将伸长又折叠回来。构成局域的分叉甚至是混沌。 ·几何示意图如下:
非线性物理:混沌物理 • 帐篷映射: • 锯齿映射: • 这两类映射具有局域演变的两个特点:伸长与折叠。 • 帐篷映射第一半是驱动过程,具有伸长性质;后一半是耗散反馈 过程,将伸长又折叠回来。构成局域的分叉甚至是混沌。 • 几何示意图如下:

非线性物理:混沌物理 伸长 折叠 2xn,0≤xn≤1/2 xn+1=T(xn)= 2-2xn,1/2<xn≤1 ·锯齿映射显得更为有趣:将x看成角变量,映射是圆上的映射, x从0到1对应于旋转一周,映射前一半是圆周伸长一倍,后一 半将圆周扭转成8字型,再折叠成近似重合的一个圆:
非线性物理:混沌物理 • 锯齿映射显得更为有趣:将 x 看成角变量,映射是圆上的映射, x 从 0 到 1 对应于旋转一周,映射前一半是圆周伸长一倍,后一 半将圆周扭转成 8 字型,再折叠成近似重合的一个圆:
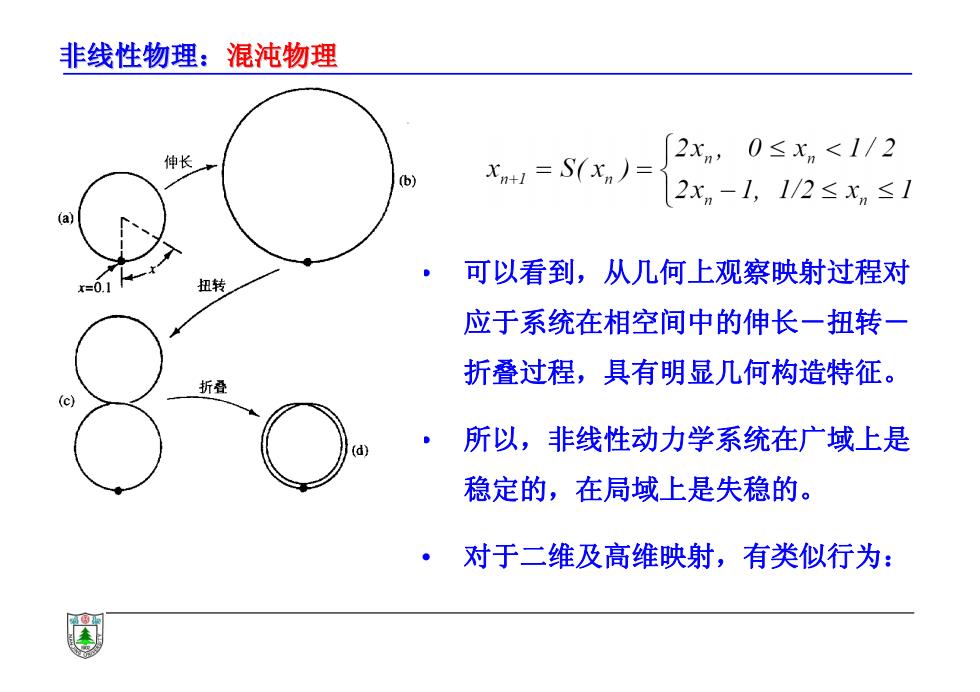
非线性物理:混沌物理 伸长 (6) x1=S(xn)= 2xn,0≤x,<1/2 2xn-1,1/2≤xn≤1 a 扭转 可以看到,从几何上观察映射过程对 应于系统在相空间中的伸长一扭转一 折叠过程,具有明显几何构造特征。 析叠 (c) (d) ·所以,非线性动力学系统在广域上是 稳定的,在局域上是失稳的。 ·对于二维及高维映射,有类似行为:
非线性物理:混沌物理 • 可以看到,从几何上观察映射过程对 应于系统在相空间中的伸长-扭转- 折叠过程,具有明显几何构造特征。 • 所以,非线性动力学系统在广域上是 稳定的,在局域上是失稳的。 • 对于二维及高维映射,有类似行为:
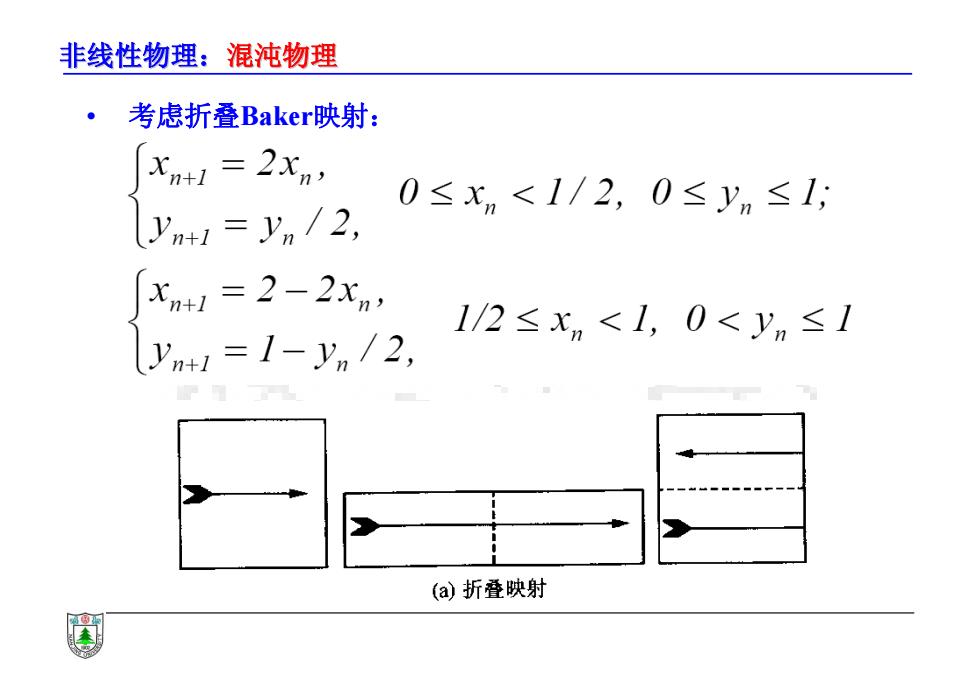
非线性物理:混沌物理 ·考虑折叠Baker映射: Xn+l=2Xn, 0≤xn<1/2,0≤yn≤1, n yn/2, Xn1=2-2xn, 1/2≤xm<1,0<yn≤1 yn+1=1-yn/2, (a)折叠映射
非线性物理:混沌物理 • 考虑折叠Baker映射: