南京大学：《非线性物理学》课程电子教案（课件讲稿）非线性物理混沌物理3/4

非线性物理：混沌物理 周期轨道与混沌： 前面几小节讨论了非线性动力系统演化的多样性、分叉的基本概 念及表征、非线性系统演化的几何特征和广域边界的分形特征。 下面开始讨论混沌发生本身的演化过程。我们最普遍的认识是： 混沌系统是周期分叉导致，如果所有周期轨道在演化过程中都失 稳，则混沌就不可避免。 以帐篷映射和锯齿映射为例来说明迭代过程中的周期轨道行为。 2xn,0≤xmn≤1/2 2xn,0≤xn<1/2 =T(xn)= =S(x)= 2-2xn,1/2<xn≤1 2xm-1,1/2≤xn≤1

非线性物理：混沌物理 周期轨道与混沌： • 前面几小节讨论了非线性动力系统演化的多样性、分叉的基本概 念及表征、非线性系统演化的几何特征和广域边界的分形特征。 • 下面开始讨论混沌发生本身的演化过程。我们最普遍的认识是： 混沌系统是周期分叉导致，如果所有周期轨道在演化过程中都失 稳，则混沌就不可避免。 • 以帐篷映射和锯齿映射为例来说明迭代过程中的周期轨道行为

非线性物理：混沌物理 帐篷映射的两次迭代TPy与多次迭代下mx)轨道如下图示： b】 ·TPx)与y=x有四个交点，x=0和=23为周期1交点；x=2/5和=4/5 为周期2交点。x-→2/5→4/5-→2/5-→4/5.，Tmx)与y=x的交点及 其对应的周期数会更多，与m相关。 因为这些交点的斜率分别为入=2和入=4，因此都不稳定

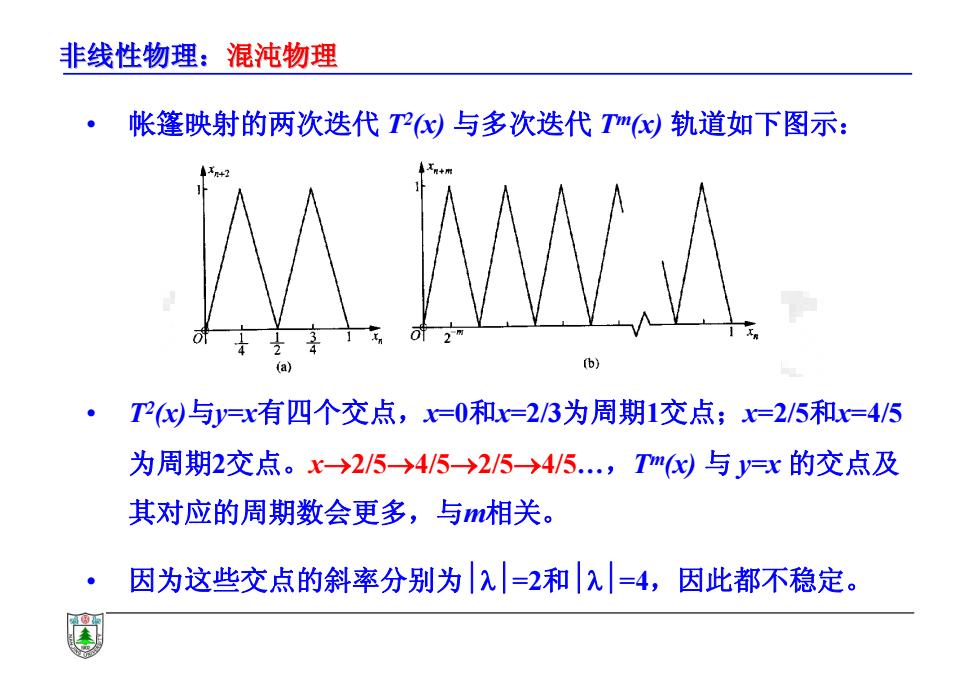
非线性物理：混沌物理 • 帐篷映射的两次迭代 T2(x) 与多次迭代 Tm(x) 轨道如下图示： • T2(x)与y=x有四个交点，x=0和x=2/3为周期1交点；x=2/5和x=4/5 为周期2交点。x2/54/52/54/5…，Tm(x) 与 y=x 的交点及 其对应的周期数会更多，与m相关。 • 因为这些交点的斜率分别为=2和=4，因此都不稳定

非线性物理：混沌物理 锯齿映射的二次和多次迭代Sx)、Smx)图示如下： n+ 用中 02m2×2 (a) (b) ·S)与=x有四个交点，x=0和=1为周期1交点；x=13和=23为 周期2交点，x→1/3→23→1/3→23..，S"x)与y=x的交点及其 对应的周期数会更多，与m相关。 同理，这些交点也是不稳定的

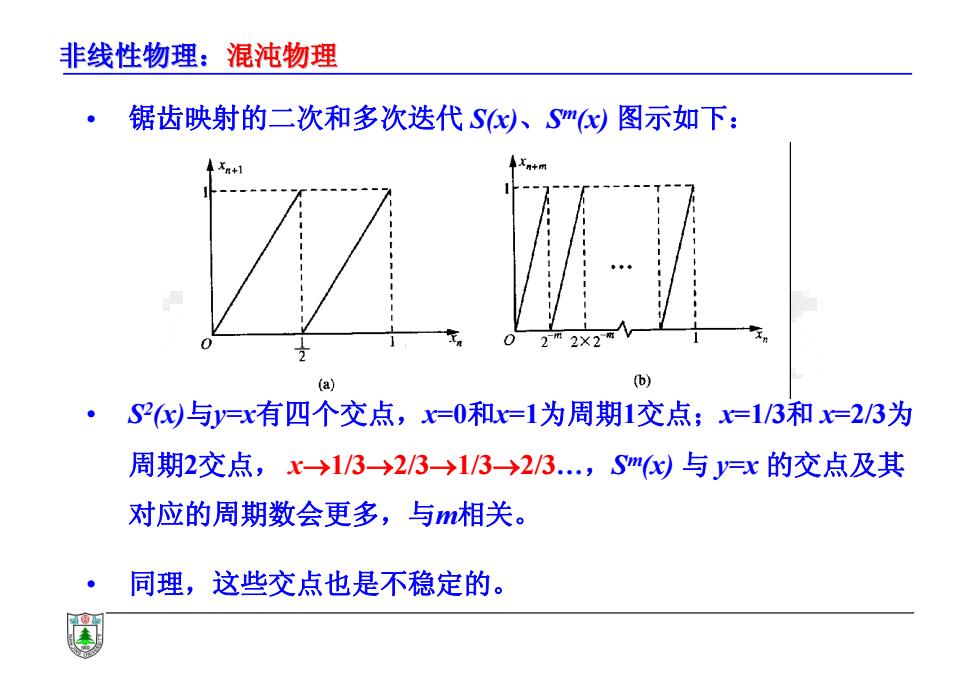
非线性物理：混沌物理 • S2(x)与y=x有四个交点，x=0和x=1为周期1交点；x=1/3和 x=2/3为 周期2交点， x1/32/31/32/3…，Sm(x) 与 y=x 的交点及其 对应的周期数会更多，与m相关。 • 同理，这些交点也是不稳定的。 • 锯齿映射的二次和多次迭代 S(x)、Sm(x) 图示如下：

非线性物理：混沌物理 对于Tmx)及Smx)之类，如何判断这些轨道交点的周期数？一种 有效方法是以二进制数来表示，非常有趣！ 。 设初值是x0.u42344,其中a非0即1。 按照锯齿映射S,2x,代表小数点向右移动一位，即ra234…, 如x<0.5,a,0,迭代一次得到r=ur234.=0.a234…;如 x≥0.5，a-1,按照迭代要求得到x0a34-1=0.a234.。锯 齿映射就是每次迭代小数点向右移动一位，整数部分取0。 。】 对帐篷映射T,x<0.5时迭代与上相同，x20.5时，x=2-2x,1- (2x1)=1-Sc),即将0.a2304.中的0和1对易，0-→1,1→0

非线性物理：混沌物理 • 对于Tm(x)及Sm(x)之类，如何判断这些轨道交点的周期数？一种 有效方法是以二进制数来表示，非常有趣！ • 设初值是 x0=0.a1a2a3a4…，其中ai非0即1。 • 按照锯齿映射S，2x0代表小数点向右移动一位，即a1.a2a3a4…， 如x0<0.5，a1=0，迭代一次得到x1=a1.a2a3a4…= 0.a2a3a4… ；如 x00.5，a1=1，按照迭代要求得到x1=a1.a2a3a4…-1=0.a2a3a4…。锯 齿映射就是每次迭代小数点向右移动一位，整数部分取0。 • 对帐篷映射T，x0<0.5时迭代与上相同， x00.5时，x1=2-2x0=1- (2x0-1)=1-S(x0)，即将0.a2a3a4…中的0和1对易，01，10

非线性物理：混沌物理 例如：x=0.101101>0.5,2x=1.01101-→0.01101，x产2- 2x=0.10010。 ,下面可以来分析锯齿映射的初值x对应的周期数了。 设x=0.1010101010..=23=0.10,x=0.0101010..=1/3=0.01;迭代 在0.10和0.01之间循环，说明是周期2轨道。 ·对于x=4/7=0.100,x=1/7=0.001,x2=2/7=0.010,依此类推，周 期3轨道。 如果x)0.a0203…up00203…up.=0.4142g…Lp,对应周期P轨道

非线性物理：混沌物理 • 例如：x0=0.101101>0.5，2x0=1.011010.01101，x1=2- 2x0=0.10010。 • 下面可以来分析锯齿映射的初值x0对应的周期数了。 • 设x0=0.1010101010…=2/3=0.10，x1=0.0101010…=1/3=0.01；迭代 在0.10和0.01之间循环，说明是周期2轨道。 • 对于x0=4/7=0.100，x1=1/7=0.001，x2=2/7=0.010，依此类推，周 期3轨道。 • 如果x0=0.a1a2a3…aPa1a2a3…aP…=0.a1a2a3…aP，对应周期P轨道