
第22章量子力学基础 §22.1实物粒子的波动性 §22.2波函数及统计解释 §22.3不确定性关系 §22.4薛定谔方程 §22.5力学量算符的本征值问题 §22.6薛定谔方程的应用 §22.7氢原子量子理论 §22.8电子的自旋泡利不相容原理
§22.1 实物粒子的波动性 §22.2 波函数及统计解释 §22.3 不确定性关系 §22.4 薛定谔方程 §22.6 薛定谔方程的应用 §22.5 力学量算符的本征值问题 §22.7 氢原子量子理论 §22.8 电子的自旋 泡利不相容原理 第 22 章 量子力学基础

§22.6薛定谔方程的应用 步骤: ·确定粒子的哈密顿量; ·在全空间写出粒子的能量本征方程; ·利用波函数的自然条件确定能量本征值和波函 数。 处理的问题: ·势阱中的粒子—粒子被束缚在某势场中; ·势垒对粒子的散射一自由粒子入射到某势场中
§22.6 薛定谔方程的应用 • 确定粒子的哈密顿量; 步骤: • 在全空间写出粒子的能量本征方程; • 利用波函数的自然条件确定能量本征值和波函 数。 处理的问题: • 势阱中的粒子——粒子被束缚在某势场中; • 势垒对粒子的散射——自由粒子入射到某势场中
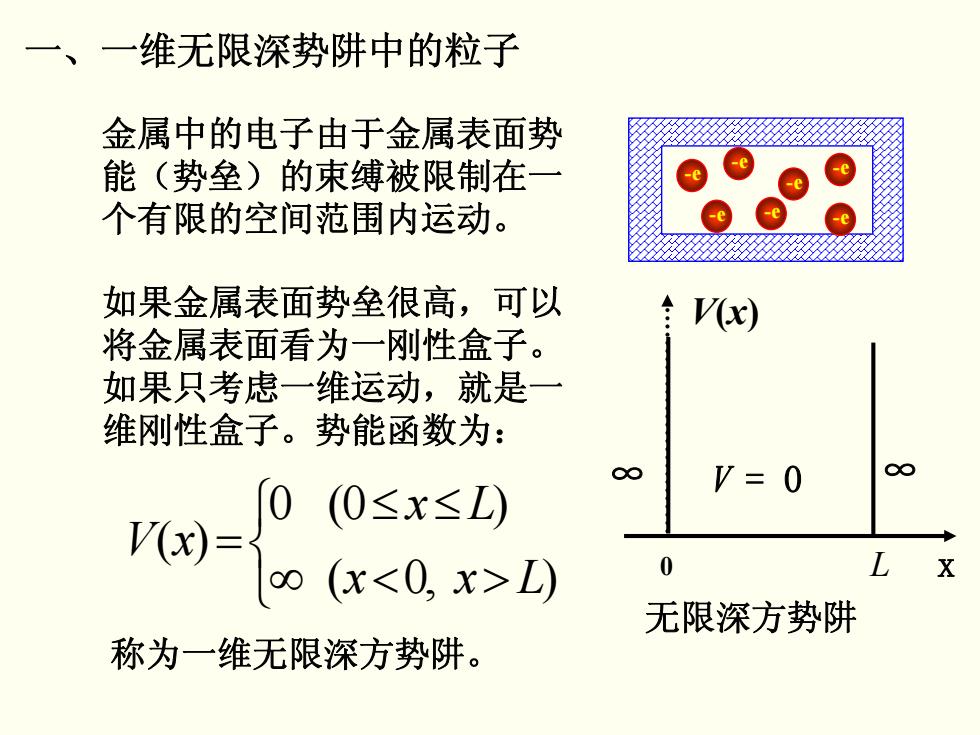
一、一维无限深势阱中的粒子 金属中的电子由于金属表面势 能(势垒)的束缚被限制在一 个有限的空间范围内运动。 如果金属表面势垒很高,可以 V(x) 将金属表面看为一刚性盒子。 如果只考虑一维运动,就是一 维刚性盒子。势能函数为: 0(0≤x≤L) V=0 V(x)= o(x<0,x>L) L 无限深方势阱 称为一维无限深方势阱
一、一维无限深势阱中的粒子 金属中的电子由于金属表面势 能(势垒)的束缚被限制在一 个有限的空间范围内运动。 称为一维无限深方势阱。 -e -e -e -e -e -e -e 如果金属表面势垒很高,可以 将金属表面看为一刚性盒子。 如果只考虑一维运动,就是一 维刚性盒子。势能函数为: ∞ V = 0 ∞ V(x ) x 无限深方势阱 0 L ⎩ ⎨ ⎧ ><∞ ≤≤ = ) ,0( )0( 0 )( Lxx Lx xV

·在势阱内,定态薛定谔方程 2mdx2 (x)=E(x) :V(x) 令 k2=2mE 得 h2 d9+k2=0 V=0 dx2 0 X 解为: 无限深方势阱 Φ(x)=Csin(kc+δ) (1) 待定常数C和8解由波函数的自然条件确定
• 在势阱内,定态薛定谔方程 令 2 2 2hmE k = 得 解为: 待定常数C 和δ解由波函数的自然条件确定。 )()( dd 2 2 i i 22 Φ x Φ xE xm − h = 0 d d i 2 2 i 2 k Φ =+ x Φ Φi = kxCx +δ 1 )sin()( )( ∞ V = 0 ∞ V(x) x 无限深方势阱 0 L

·在势阱外,定态薛定谔方程 该方程的解只能是: 少.(x)≡0 (2) ·波函数在阱壁上的连续条件、本征能量 Φ(0)=Φ.(0)=0 (3) Φ(L)=Φ.(L)=0 (4)
• 波函数在阱壁上的连续条件、本征能量 该方程的解只能是: Φe x ≡ 2 0)( )( • 在势阱外,定态薛定谔方程 Φi =Φe = 3 0)0()0( )( Φi =Φe LL = 4 0)()( )( )()( dd 2 2 e e 22 xEx xm ⎟⎟ = ΦΦ⎠⎞ ⎜⎜⎝⎛ ∞+− h