AKKD3)磁化电流例 3.2.3判断磁化电流的方向。体磁化电流J.-VxM淘面磁化电流K,=Mxe.结论:Ka有磁介质存在时场中任一点的B是自由电流和磁化电流共同作用在真空中产生的磁场。磁化电流具有与传导电流相同的磁效应4)磁偶极子与电偶极子对比电量模型产生的电场与磁场电偶极子fgP,=-V.P+o,=P.enb=dg一磁偶极子K.=MxenJm=VxMm=I.ds
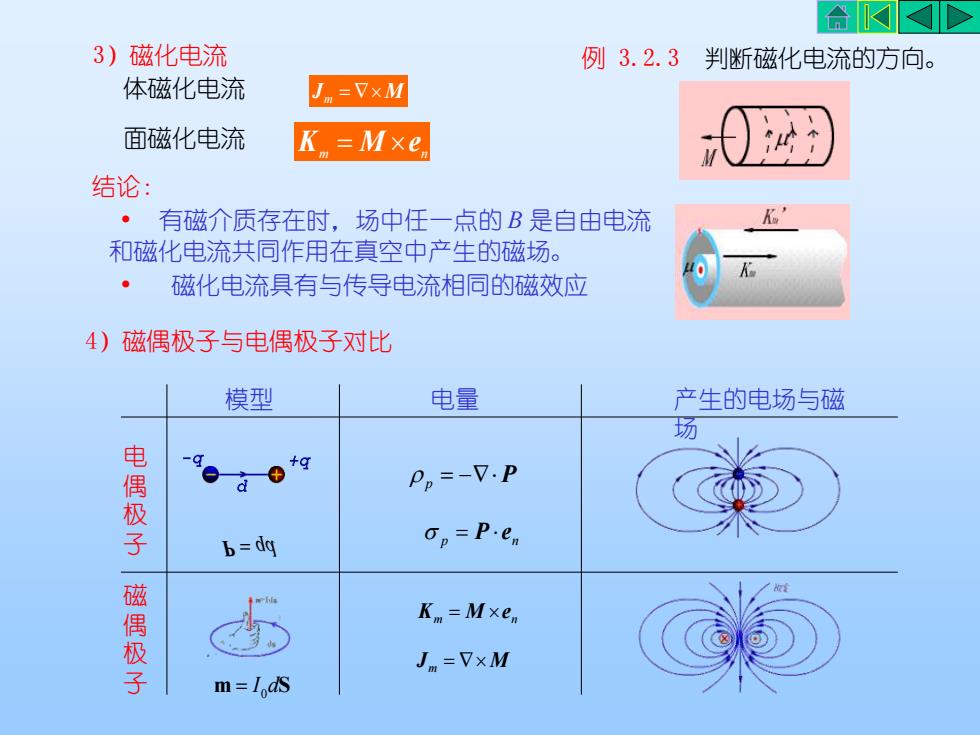
3)磁化电流 4)磁偶极子与电偶极子对比 体磁化电流 Jm = M 模型 电量 产生的电场与磁 场 电 偶 极 子 磁 偶 极 子 P = qd m = I 0 dS p = − P p n = P e m n K = M e Jm = M m n 面磁化电流 K = M e • 有磁介质存在时,场中任一点的 B 是自由电流 和磁化电流共同作用在真空中产生的磁场。 结论: • 磁化电流具有与传导电流相同的磁效应 例 3.2.3 判断磁化电流的方向
AKKD3.一般形式的安培环路定律有磁介质时(B.dl=μol=o(I+1m)=μo1+μo[Jmds将J.=V×M 代入上式, 得f Bdl=I+[(V×M),ds=I+f,M·dlo(B-M)dl=I移项后oB-M定义磁场强度H=A/mofH.dl-I则有说明:·H的环量仅与环路交链的自由电流有关。图3.2.18H与成右螺旋关系·环路上任一点的H是由系统全部载流体产生的。·电流的正、负仅取决于环路与电流的交链是否满足右手螺旋关系,是为正,否为负。H.dl=1→1(VxH).ds=J.dsVXH-J恒定磁场是有旋的厨思考事图示中H,=H=H,吗?它们的环量相等吗?图3.2.19H的分布与磁介质有关
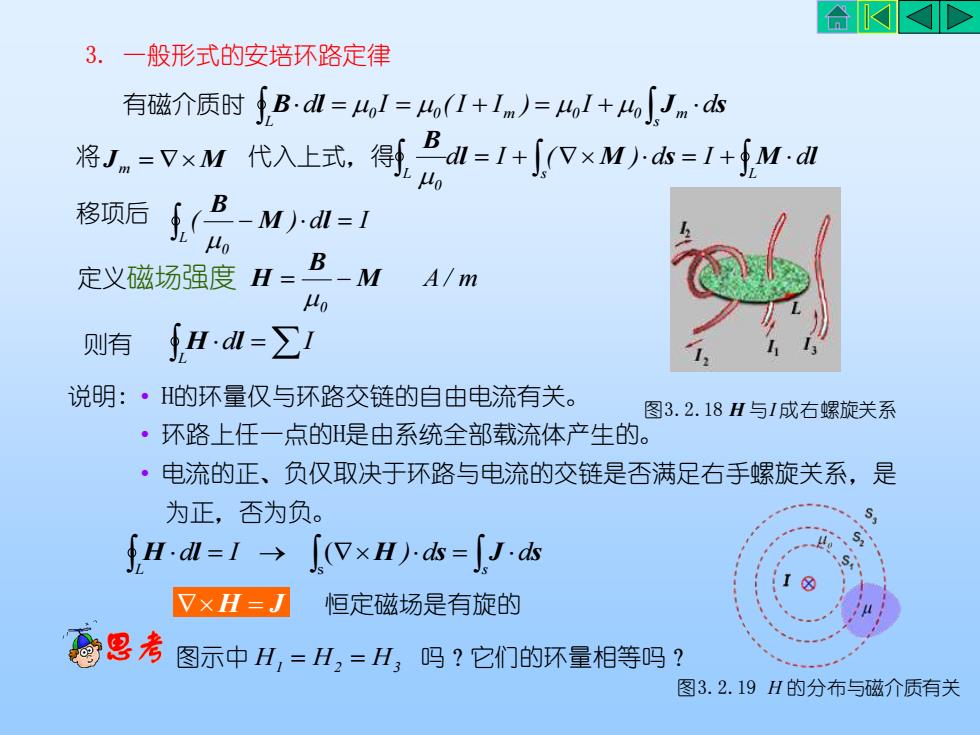
3. 一般形式的安培环路定律 B dl I ( I I ) I J ds s 0 0 m 0 0 m L = = + = + 有磁介质时 将 Jm = M 代入上式,得 l M s M l B d I ( ) d I d L s L 0 = + = + 移项后 ( ) d I L 0 − = M l B 定义磁场强度 A / m 0 M B H = − 则有 d =I L H l 说明: • H的环量仅与环路交链的自由电流有关。 • 环路上任一点的H是由系统全部载流体产生的。 • 电流的正、负仅取决于环路与电流的交链是否满足右手螺旋关系,是 为正,否为负。 H dl I H ) ds J ds L s = → = s ( H = J 恒定磁场是有旋的 图3.2.19 H 的分布与磁介质有关 图3.2.18 H 与I 成右螺旋关系 图示中 H1 = H2 = H3 吗?它们的环量相等吗?

AKD4.B与H的构成关系实验证明,在各向同性的线性磁介质中M=x.H式中xm磁化率,无量纲量,代入H=B/uo-M中B=μo(H+M)=μH(I+x)=μHH=μH式中u,相对磁导率,无量纲,μ=μo,单位H/mB-H构成关系5.H的旋度fH.dl-=1-JJ.ds→[rVxH)ds=JJ.ds恒定磁场是有旋的积分式对任意曲面S都成立,则V×H=J例3.2.4:一矩形截面的镯环,如图示,试求气隙中的B和H。解:在镯环中-→0B=H有限,故H=0取安培环路(与交链),由H·dl=NI,得NIB=HoNIH=H.ro=NIroeo24ro图3.2.20镯环磁场分布
4. B与H的构成关系 实验证明,在各向同性的线性磁介质中 式中 —— 磁化率,无量纲量,代入 中 M = xmH m x H = B 0 − M B = 0 ( H + M ) = 0H(1+ xm ) = 0 rH = H 式中 r —— 相对磁导率,无量纲, = 0 r ,单位 H/m。 构成关系 B = H 例3.2.4: 一矩形截面的镯环,如图示,试求气隙中的B和H。 图3.2.20 镯环磁场分布 解:在镯环中, → r , B = H 有限,故H = 0。 取安培环路(与I交链),由 L H dl = NI ,得 H r = NI , r NI H = e B e r NI 0 = 5. H的旋度 = = L s H dl I J ds → = s s ( H ) ds J ds 积分式对任意曲面S都成立,则 H = J 恒定磁场是有旋的

合KD例 3.2.4 有一磁导率为μ,半径为a 的无限长导磁圆柱,其轴线处有无限长的线电流I,圆柱外是空气(μo),如图所示。试求圆柱内外的B,H与M的分布。解:磁场为平行平面场,且具有轴对称性,应用安培环路定律,得fH dl = 2元pH, =1/LloH0<p<8e磁场强度2元p1M-MoBp<aH(p)H1M=磁化强度2元uu0a<p<ul0<p<ae2元pB(o)B=磁感应强度Hola<p<8I2元p奇思考PM(pA导磁圆柱内P=0处有磁化电流12元aKmI吗?q=a处有面磁化电流K吗?为什么?图3.2.22长直导磁圆柱的磁化电流图3.2.21磁场分布
例 3.2.4 有一磁导率为 µ ,半径为a 的无限长导磁圆柱,其轴线处有无限长的 线电流I,圆柱外是空气(µ0 ),如图所示。试求圆柱内外的 B,H 与 M 的分布。 解:磁场为平行平面场,且具有轴对称性,应用安培环路定律, 得 d 2 H I l = = H l 磁场强度 = 0 2 I H e 磁化强度 = − H = B M − 0 a a 2 I 0 e 磁感应强度 B = a I a I 2 0 2 0 e 图3.2.21 磁场分布 图3.2.22 长直导磁圆柱 的磁化电流 导磁圆柱内 = 0 处有磁化电流 Im 吗? = a 处有面磁化电流 Km吗? 为什么?

AKKD3.3恒定磁场的基本方程·分界面上的衔接条件3.3.1恒定磁场的基本方程恒定磁场的基本方程表示为B.dS=0V·B=0(磁通连续原理)(无源)fH.dl=1VxH=J(有旋)(安培环路定律)B=uH媒质的性能方程恒定磁场是有旋无源场,电流是激发磁场的涡旋源例3.3.1试判断(a)F=axe,+byex(b)F,=ape。能否表示为一个恒定磁场?10aFlyOFi+(b)V.E,=(pF2p)(a)V.F,=解:papaxya(pdp)=2a±0=0+0=0papF可以表示为恒定磁场。F,不可能表示恒定磁场
3.3 恒定磁场的基本方程 • 分界面上的衔接条件 3.3.1 恒定磁场的基本方程 媒质的性能方程 B = H 例 3.3.1 试判断 ( a ) F1 = axey + byex ( b ) F2 = a e 能否表示为一个恒定磁场? F2不可能表示恒定磁场。 ( d ) 2a 0 1 = = ( F ) 1 ( b ) 2 F2 = 恒定磁场的基本方程表示为 = S B dS 0 d I l = H l (磁通连续原理) (安培环路定律) B =0 H = J (无源) (有旋) 恒定磁场是有旋无源场,电流是激发磁场的涡旋源 0 0 0 y F x F a 1x 1y 1 = + = + = ( ) F F1可以表示为恒定磁场。 解: