西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第三章 恒定磁场

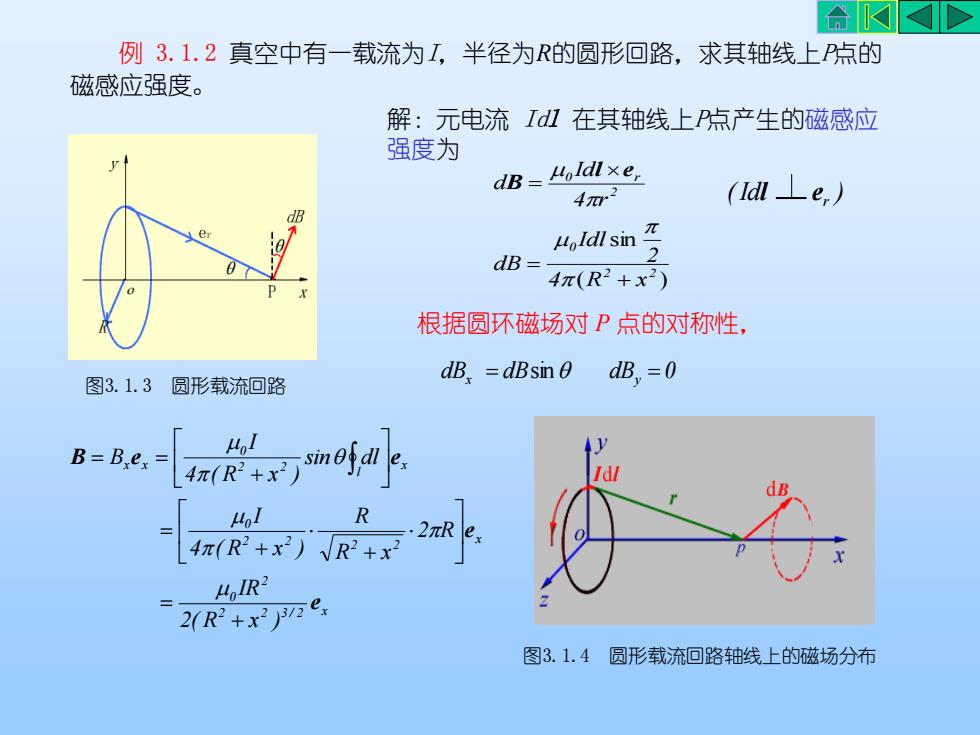
AKKD例3.1.2真空中有一载流为I，半径为R的圆形回路，求其轴线上P点的磁感应强度。解：元电流Id1在其轴线上P点产生的磁感应强度为dB= Holdl xe,(Idl Le,)4元2Moldlsin"dB4元（R+×）根据圆环磁场对P点的对称性，dB,=0dB, =dBsin 0图3.1.3圆形载流回路Ho!AJsinegdlB=Ber4元（R+x）IdlRHol2元R4元（R+x）R+×H,R?2(R+xe图3.1.4圆形载流回路轴线上的磁场分布

2 2 3 / 2 x 2 0 x 2 2 2 2 0 x l 2 2 0 x x 2( R x ) IR 2 R R x R 4 ( R x ) I sin dl 4 ( R x ) I B e e B e e + =        +  + =       + = =         解：元电流 Idl 在其轴线上P点产生的磁感应 强度为 ( ) sin 2 2 0 2 0 r 4 R x 2 Idl dB 4 r Id d + =  =      l e B ( Id ) r l e 例 3.1.2 真空中有一载流为I，半径为R的圆形回路，求其轴线上P点的 磁感应强度。 图3.1.4 圆形载流回路轴线上的磁场分布 根据圆环磁场对 P 点的对称性， dB dB dB 0 x = sin  y = 图3.1.3 圆形载流回路

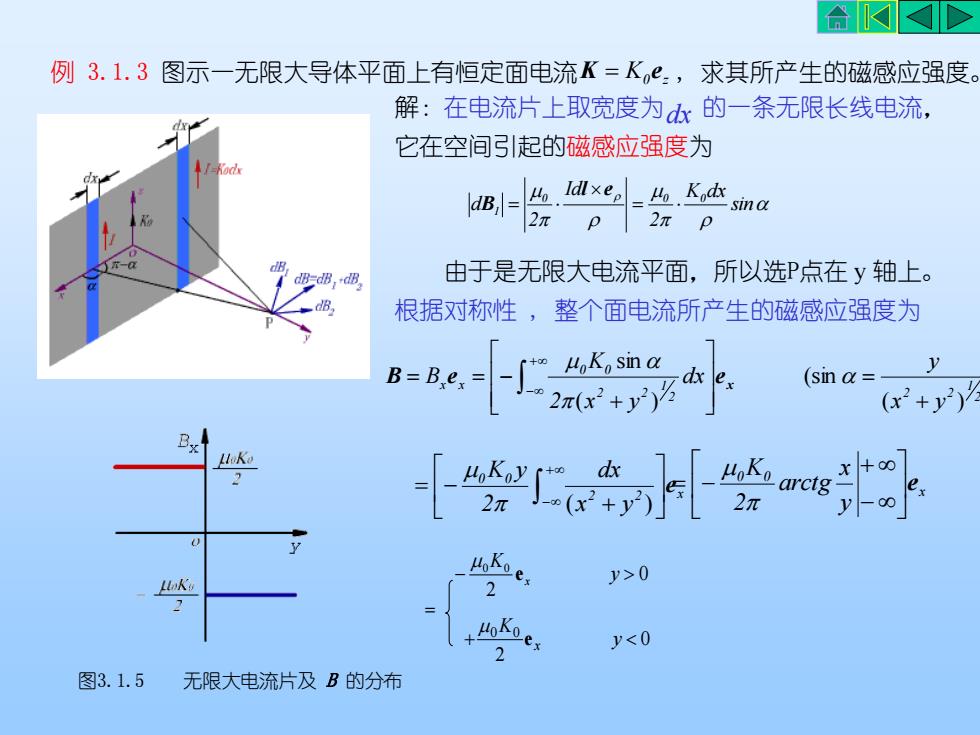
合KD例3.1.3图示一无限大导体平面上有恒定面电流K=K.e，求其所产生的磁感应强度。解：在电流片上取宽度为dx的一条无限长线电流，它在空间引起的磁感应强度为MoIdlxep-HoK,dxdB,sina2元2元PP由于是无限大电流平面，所以选P点在y轴上。B=dB,dB根据对称性，整个面电流所产生的磁感应强度为HKsinαyB=Ber=(sinα:exle2(x+y(x+y)Bx4LuKo-8dxHoKHoKoyarctg(x+y)2元2元VMoKoy>0eLok2+HoKoJ<OE2图3.1.5无限大电流片及B的分布

由于是无限大电流平面，所以选P点在 y 轴上。 根据对称性 , 整个面电流所产生的磁感应强度为 ) ( ) (sin ( ) sin 2 1 2 2 2 1 2 2 0 0 x x x y y dx 2 x y K B + =         + = = −  + −     x B e e 例 3.1.3 图示一无限大导体平面上有恒定面电流 K = K0 ez , 求其所产生的磁感应强度。 解：在电流片上取宽度为 的一条无限长线电流， 它在空间引起的磁感应强度为         sin K dx 2 Id 2 d 0 0 0 1 =   =  l e B dx 0 2 0 0 + y  K x e  0 2 0 0 − y  K x e  = 2 2 x 0 0 x y dx 2 K y e      + = −  + −  ( )  x 0 0 y x arctg 2 K  e      − +  = −   图3.1.5 无限大电流片及 B 的分布

AKKD3.2磁通连续性原理·安培环路定律3.2.1磁通连续性原理R=r-r1. 恒定磁场的散度(x.y',z)P(x,V2)可从Biot-SavartLaw 直接导出恒定磁场B的散度B(x,y,2)=o,(x,y)xeraY4元J度V.B(x,y,a)=v.J(xy)xedv两边取散度4TJV图3.2.1计算体电流的磁场yV.(AxC)=C.VXA-A.VxC矢量恒等式[(xy((((y则所以V·B=0表明B是无头无尾的闭合线，恒定磁场是无源场。（在任意媒质中均成立）V·B=0可以作为判断一个失量场能否成为恒定磁场的必要条件

3.2 磁通连续性原理 • 安培环路定律 3.2.1 磁通连续性原理 矢量恒等式 ( AC ) = C  A− AC 所以 B = 0 表明 B 是无头无尾的闭合线，恒定磁场是无源场。（在任意媒质中均成立） ) dV r 1 ( x , y ,z ) ( 4 V 0        =        J   两边取散度 dV r x y z e 4 x y z V 2 0 r       =    ( , , ) ( , , ) J B   可从 Biot-Savart Law 直接导出恒定磁场 B 的散度。 dV r x y z 4 x y z V 2 0 r      =   J e B ( , , ) ( , , )   1. 恒定磁场的散度 则 ) 0 r 1 ) ( x , y ,z ) ( x , y ,z ) ( r 1 ) ( r 1 ( x , y ,z ) ( =      =      −             J     J J 0 0 B =0 可以作为判断一个矢量场能否成为恒定磁场的必要条件。 图3.2.1 计算体电流的磁场

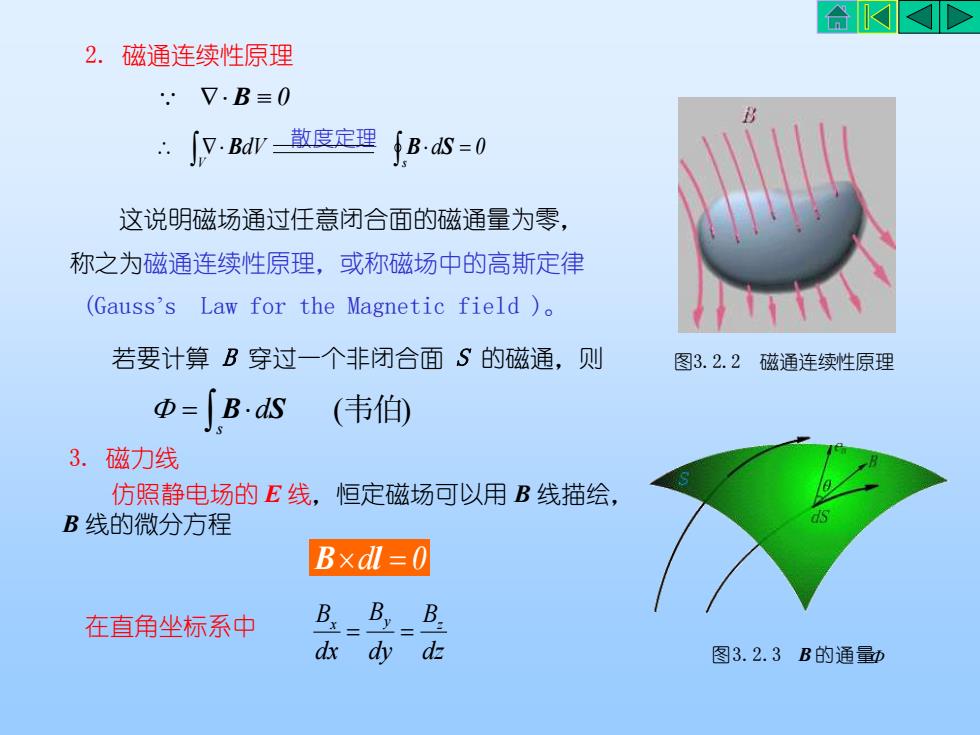
合KKD2.磁通连续性原理: V.B=0：[·BdV_散度定理$B.dS=0这说明磁场通过任意闭合面的磁通量为零称之为磁通连续性原理，或称磁场中的高斯定律(Gauss'sLaw for the Magnetic field )。若要计算B穿过一个非闭合面 S的磁通，则图3.2.2磁通连续性原理Φ=B.ds (韦伯)3.磁力线仿照静电场的E线，恒定磁场可以用B线描绘，B线的微分方程Bxdl=0B_By_B在直角坐标系中dxdydz图3.2.3B的通量D

2. 磁通连续性原理 这说明磁场通过任意闭合面的磁通量为零， 称之为磁通连续性原理，或称磁场中的高斯定律 (Gauss’s Law for the Magnetic field )。 仿照静电场的 E 线，恒定磁场可以用 B 线描绘， B 线的微分方程 Bdl = 0 在直角坐标系中 dz B dy B dx Bx y z = =  B  0 dV d 0 V s    =   B 散度定理 B S 图3.2.2 磁通连续性原理 图3.2.3 B 的通量 若要计算 B 穿过一个非闭合面 S 的磁通，则 (韦伯)  =  s  B dS 3. 磁力线

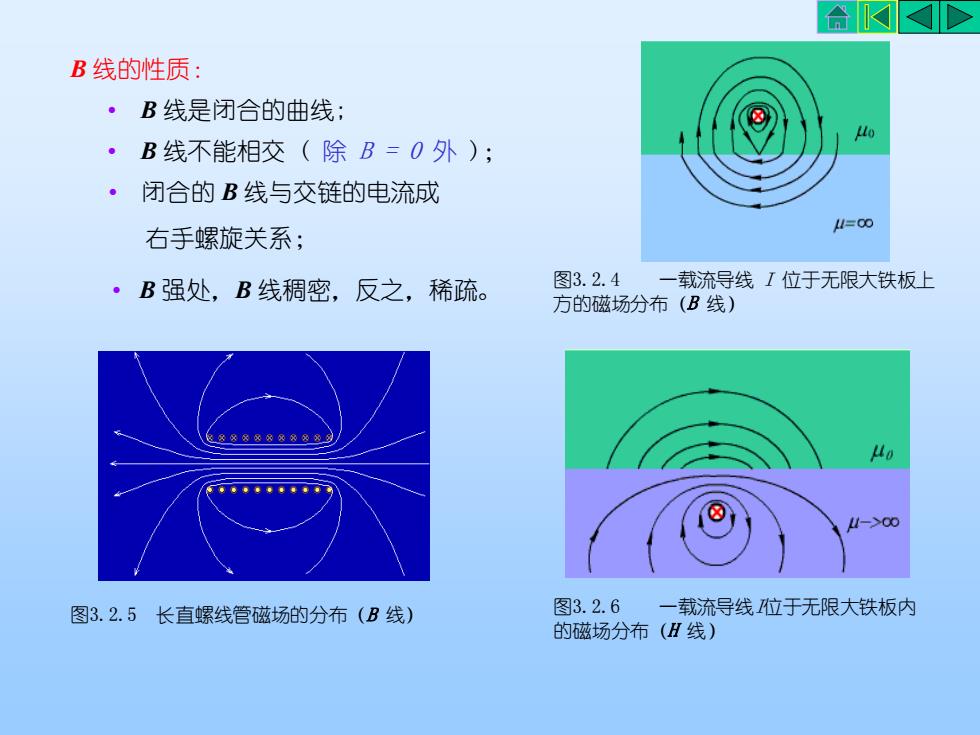
AKKDB线的性质：B线是闭合的曲线；LB线不能相交（除B=0外）；闭合的B线与交链的电流成1=00右手螺旋关系；图3.2.4一载流导线I位于无限大铁板上B强处，B线稠密，反之，稀疏。方的磁场分布（B线）L>00图3.2.6一载流导线位于无限大铁板内图3.2.5长直螺线管磁场的分布（B线）的磁场分布（H线）

B 线的性质： • B 线是闭合的曲线; • B 线不能相交 ( 除 B = 0 外 )； • 闭合的 B 线与交链的电流成 右手螺旋关系； • B 强处，B 线稠密，反之，稀疏。 图3.2.4 一载流导线 I 位于无限大铁板上 方的磁场分布（B 线） 图3.2.5 长直螺线管磁场的分布（B 线） 图3.2.6 一载流导线I位于无限大铁板内 的磁场分布（H 线）