
自动控制原理 第五章频域分析法一频率法 -1 0 1 2 1go 0.1 0.2 0.4 2 4 10 2040 100 十倍频程 十倍频程 (a)对数分度 0 2 3 (b)线性分度 对数分度中任一两个刻度之间的距离为: 1go,-1g@Ig 02 课本P172 表5-1:1g2=0.301,g3=0.477,g4=0.602,lg5=0.699.…
自动控制原理 第五章 频域分析法-频率法 对数分度中任一两个刻度之间的距离为: 2 2 1 1 lg lg lg − = lg 2 0.301,lg 3 0.477,lg 4 0.602,lg 5 0.699 = = = = 课本P172 表5-1:

自动控原理 第五章频域分折法一频率法 采用对数坐标图的优点是: (1)对数刻度实现了横坐标的非线性压缩,扩 大了研究问题的视野。即在同一图纸上可同 时研究低中高频特性。 (2)20gA(o)可以将幅值的乘除转化为加减, 简化曲线的绘制
自动控制原理 第五章 频域分析法-频率法 采用对数坐标图的优点是: (1)对数刻度实现了横坐标的非线性压缩,扩 大了研究问题的视野。即在同一图纸上可同 时研究低中高频特性。 (2) 20lgA(ω)可以将幅值的乘除转化为加减, 简化曲线的绘制
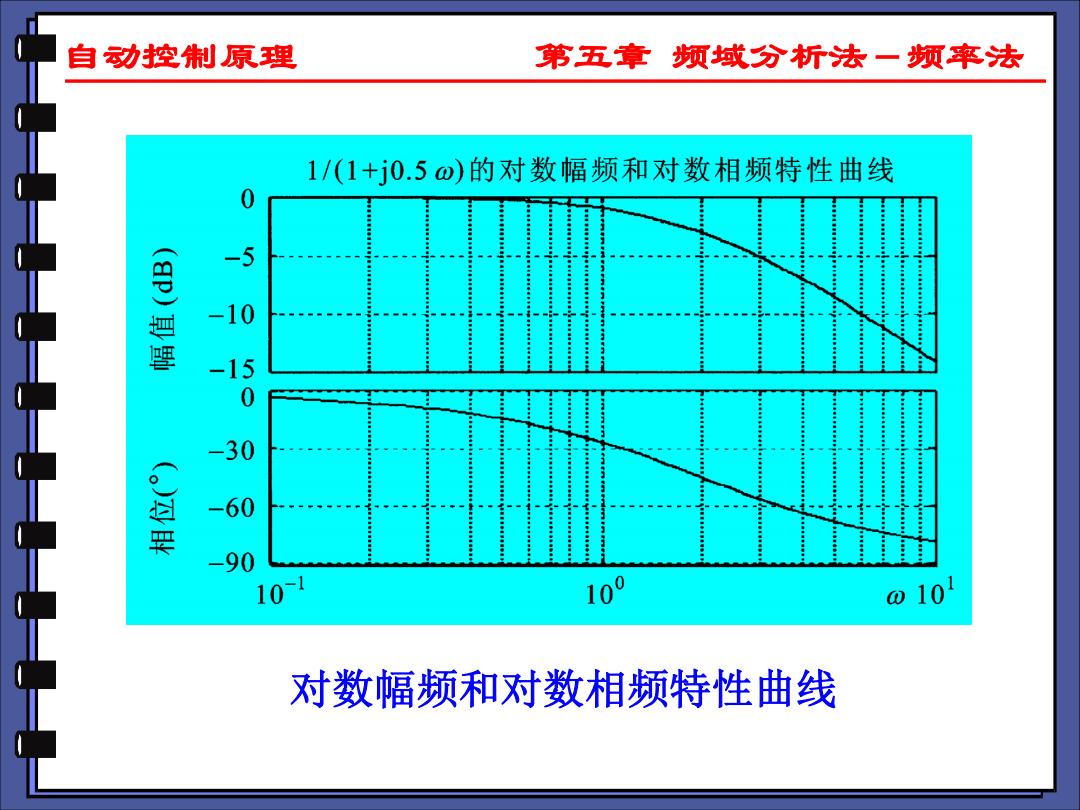
自动控原理 第五章频域分析法一频率法 1/(1+j0.5ω)的对数幅频和对数相频特性曲线 0 10 100 10 对数幅频和对数相频特性曲线
自动控制原理 第五章 频域分析法-频率法 对数幅频和对数相频特性曲线

自动控制原理 第五章 频域分析法一频率法 (3)对数幅相曲线尼柯尔斯曲线 它是由对数幅频特性和对数相频恃性合并而成的 曲线。横轴为相频0(0),纵轴为L(0).横坐标 和纵坐标均为线性刻度。 0为一个参变量标 在曲线上相应点的 旁边。 10 2 100 8060-40-20 p(awX·)
自动控制原理 第五章 频域分析法-频率法 (3)对数幅相曲线/尼柯尔斯曲线 ω为一个参变量标 在曲线上相应点的 旁边。 它是由对数幅频特性和对数相频特性合并而成的 曲线。横轴为相频φ(ω),纵轴为L(ω).横坐标 和纵坐标均为线性刻度

自动控原理 第五章频域分析法一频率法 5.2典型环节与开环系统频率特性 一、典型环节 将传递函数分解成因式乘积的形式,再对因式分类 得典型环节。典型环节分为两类:最小相位环节和 非最小相位环节。 最小相位环节 非最小相位环节 K (K>0) 1/s K(K<0) 右半平 S 1/(-T+1) 面的零 1/(Ts+1) (T>0) -Ts+1 极点 Ts+1 1/(T2s2-25Ts+1) 1/(T2s2+25Ts+1)(0<5<1) T2s2-25Ts+1 T2s2+25Ts+1
自动控制原理 第五章 频域分析法-频率法 5.2 典型环节与开环系统频率特性 一、典型环节 将传递函数分解成因式乘积的形式,再对因式分类 得典型环节。典型环节分为两类:最小相位环节和 非最小相位环节。 最小相位环节 2 2 2 2 ( 0) 1 / 1 / ( 1) ( 0) 1 1 / ( 2 1)(0 1) 2 1 K K s s Ts T Ts T s Ts T s Ts + + + + + + 非最小相位环节 2 2 2 2 (K 0) 1 / ( 1) 1 1 / ( 2 1) 2 1 K Ts Ts T s Ts T s Ts − + − + − + − + 右半平 面的零 极点