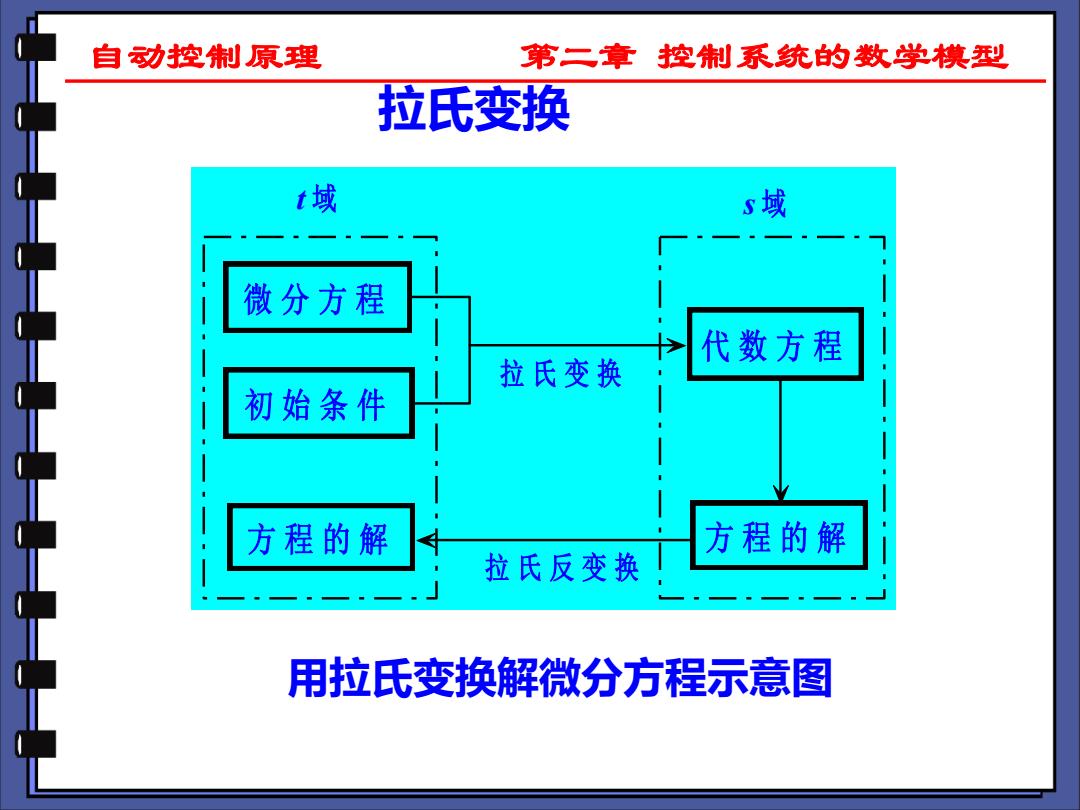
自动控制原理 第二章控制系统的数学模型 拉氏变换 t域 s域 微分方程 代数方程 拉氏变换 初始条件 方程的解 方程的解 拉氏反变换 用拉氏变换解微分方程示意图
自动控制原理 第二章 控制系统的数学模型 微 分 方 程 初 始 条 件 方 程 的 解 代 数 方 程 方 程 的 解 拉 氏 变 换 拉 氏 反 变 换 t 域 s 域 用拉氏变换解微分方程示意图 拉氏变换

自动控制原理 第二章控制系统的数学模型 拉氏变换的定义 1.定义 设函数孔)在20时有定义,如果线性积分 ∫fue"a (5=σ+jo,0>0) 存在,则由此积分所确定的函数可写为 F(s)=f(t)e"dt 见课本P26式(2-11)}
自动控制原理 第二章 控制系统的数学模型 一 、 拉氏变换的定义 1. 定义 设函数f(t)在t≥0时有定义,如果线性积分 0 ( )e dst f t t + − ( , 0) s = + j 存在,则由此积分所确定的函数可写为 - 0 ( ) ( )e dst F s f t t + = {见课本P26 式(2-11)}

自动控荆原理 第二章控制系统的数学模型 称其为函数孔)的拉普拉斯变换,并记作 F(s)=LLf(t) 代S)称为的象函数,而孔)称为尺S的原函数, 由象函数求原函数的运算称为拉氏反变换,记作 f(t)=LF(s)] {见课本P26式(2-12)}
自动控制原理 第二章 控制系统的数学模型 F s L f t ( ) [ ( )] = L F(s)称为f(t)的象函数,而f(t)称为F(s)的原函数, 由象函数求原函数的运算称为拉氏反变换,记作 1 f t L F s ( ) [ ( )] − = 称其为函数f(t)的拉普拉斯变换,并记作 {见课本P26 式(2-12)}

自动控制原理 第二章控制系统的数学模型 二、几种典型函数的拉氏变换(P32表2-3) 1.单位阶跃函数1() )个 数学表达式为 0=0= 0 其拉氏变换为 Fs)=L【f(tI=Jft)edt =小1e=elg=-0-川=月
自动控制原理 第二章 控制系统的数学模型 二、几种典型函数的拉氏变换(P32 表2-3) 1.单位阶跃函数1(t) 数学表达式为 其拉氏变换为 O t f(t) 1 0 0 0 ( ) [ ( )] ( )e d 1 1 1 1 e d e [0 1] st st st F s f t f t t t s s s + − + − − + = = = = − = − − = L 1 0 ( ) 1( ) 0 0 t f t t t = = ≥

自动控制原理 第二章控制系统的数学模型 4.指数函数em 数学表达式为 四日!o的安 0 t<0 其拉氏变换为 F()=L[e"]=∫ee dt =∫= 1 s+a
自动控制原理 第二章 控制系统的数学模型 4.指数函数e -at 数学表达式为 其拉氏变换为 e 0( ) ( ) 0 0 at t a f t t − = ≥ 为实数 0 ( ) 0 ( ) e e e d 1 e d at at st s a t F s t t s a + − − − + − + = = = = + L