
6.1.2 多元函数概念 简单说,函数依赖的自变量多于一个称为 多元函数 设D是xy平面上的集合,依照规律f,D内 任一点(x,y),有唯一z与之对应, (x,y)→z 则称f是定义在D上的二元函数,记为 一 般由几条 z=f(x,y),(x,y)∈D 光滑曲线围 成(区域) 自变量 定义域
6.1.2 多元函数概念 简单说,函数依赖的自变量多于一个称为 设 D 是xy平面上的集合,依照规律 f , D 内 多元函数 任一点 (x,y ) ,有唯一 z 与之对应, zy,x ⎯⎯→f )( z = f x y x y),(),,( ∈ D 则称 f 是定义在 D上的二元函数,记为 自变量 定义域 一般由几条 光滑曲线围 成(区域)

二元函数包括两个要素(定义域、对应规律) 例设f(x,y)=x2+y2,求f(x十y,xy) 例已知fx+y,xy)=x3+y,求f(x,) 例求z=V4-x2-y2+ln(x2+y2-1) 的定义域
例 已知 ,),( 33 +=+ yxxyyxf 求 yxf ),( 二元函数包括两个要素(定义域、对应规律) 例 设 f (x, y) = x2+y2, 求 f (x+y, x-y) 4 ln( )1 22 22 例 求 yxyxz −++−−= 的定义域

■二元函数图形(几何意义) 集合{(x,y,z)z=f(x,y),(x,y)∈D}所对应 几何图形称为二元函数的图形,一般而言是R3中 的一个曲面;曲面在xy面上的投影区域就是函数 的定义域D D
■ 二元函数图形(几何意义) 几何图形称为二元函数的图形,一般而言是R3中 集合 = ∈ Dyxx,yfzx,y,z }),(,)(){( 所对应 的一个曲面;曲面在xy 面上的投影区域就是函数 的定义域D x z y x z y D
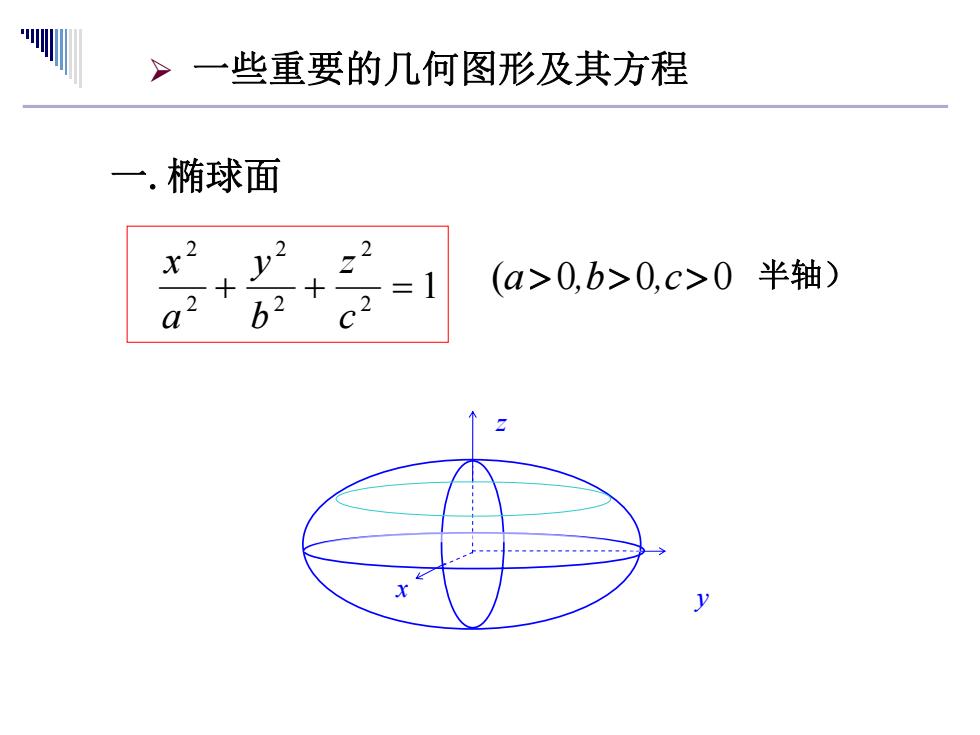
>一些重要的几何图形及其方程 一.椭球面 =1 (a>0,b>0,c>0半轴) b2 X y
¾ 一些重要的几何图形及其方程 一.椭球面 1 2 2 2 2 2 2 =++ c z b y a x ,c,ba >>> 000( 半轴) y x z

二.椭圆抛物面 +y2 a2 62 当=b,为旋转抛物面 三.双曲抛物面 x2 2 a
二.椭圆抛物面 2 2 2 2 b y a x z += x y z 当 a=b, 为旋转抛物面 三.双曲抛物面 z b y a x =− 2 2 2 2 x y z O