序列的基本运算 ·序列的基本运算 (a)序列相乘 yn] (b)序列相加 w [n]-xnly(n] w2网-n]+ym (a) (b) (c)倍乘 (d)右移位(迟延) n一网1钢—回一网 wa[n]=xn-1] (e)左移位(提前) w3(n]-Ax[n] (c) (d) (f)复制 其中(a)属于非线 t乙一w,网 m]+十一n] 性运算,(e)属 w5n闪=xn+] (e) (① 于非因果运算 图2.2.2序列运算的基本类型 11
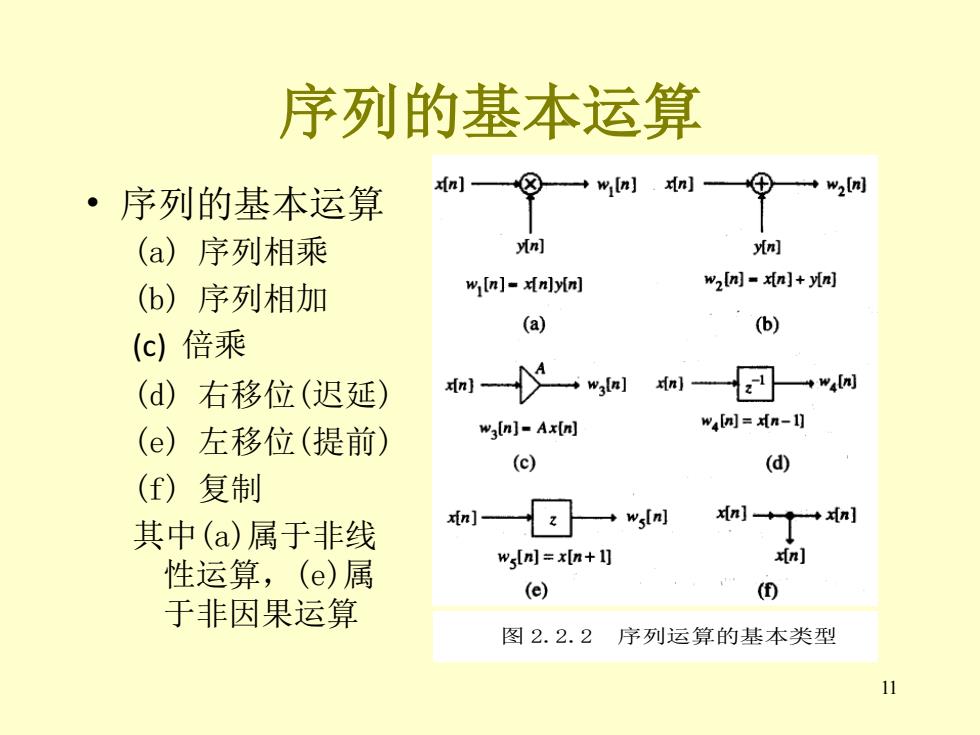
11 序列的基本运算 • 序列的基本运算 (a) 序列相乘 (b) 序列相加 (c) 倍乘 (d) 右移位(迟延) (e) 左移位(提前) (f) 复制 其中(a)属于非线 性运算,(e)属 于非因果运算 图 2.2.2 序列运算的基本类型

序列的相乘和相加运算 ·序列相乘相加子程序seqmult,seqadd编法: -将两个序列x1,x2的位置向量nl与n2对准,长 度取两者之‘合’;形成一个新的包含nl与 n2的公共位置向量n。其起点为两者中小的 起点,终点为两者中大的终点, n min(ns1,ns2):max(nf1,nf2); -将x1,x2补零,在n上延长,构成yl,y2, 一各个对应元素相乘或相加; ·yy1,*y2,(或y=y1+y2;) 12
12 • 序列相乘相加子程序seqmult,seqadd编法: – 将两个序列x1,x2的位置向量n1与n2对准,长 度取两者之‘合’;形成一个新的包含n1与 n2的公共位置向量n。其起点为两者中小的 起点,终点为两者中大的终点, n = min(ns1,ns2)::max(nf1,nf2); – 将x1,x2补零,在n上延长,构成y1,y2; – 各个对应元素相乘或相加; • y=y1,*y2; (或y=y1+y2;) 序列的相乘和相加运算

序列相加的子程序segadd n=min(min(n1),min(n2)):max(max(n1),max(n2)); %yn)的长度 ·yl=zerost(1,length(n);y2=yl;%yl,y2初始化 .y1(find((n>=min(n1))&(n<=max(n1))))=x1; %把xl补零,扩展为具有y的长度的y1 y2(find((n>=min(n2))&(n<=max(n2))))=x2; %把x2补零,扩展为具有y的长度的y2 、y=y1+y2, %序列相加 3
13 序列相加的子程序seqadd • n = min(min(n1),min(n2)):max(max(n1),max(n2)); % y(n)的长度 • y1= zeros(1,length(n)); y2 = y1; % y1,y2初始化 • y1(find((n>=min(n1))&(n<=max(n1))))=x1; % 把x1补零,扩展为具有y的长度的y1 • y2(find((n>=min(n2))&(n<=max(n2))))=x2; % 把x2补零,扩展为具有y的长度的y2 • y = y1+y2; % 序列相加

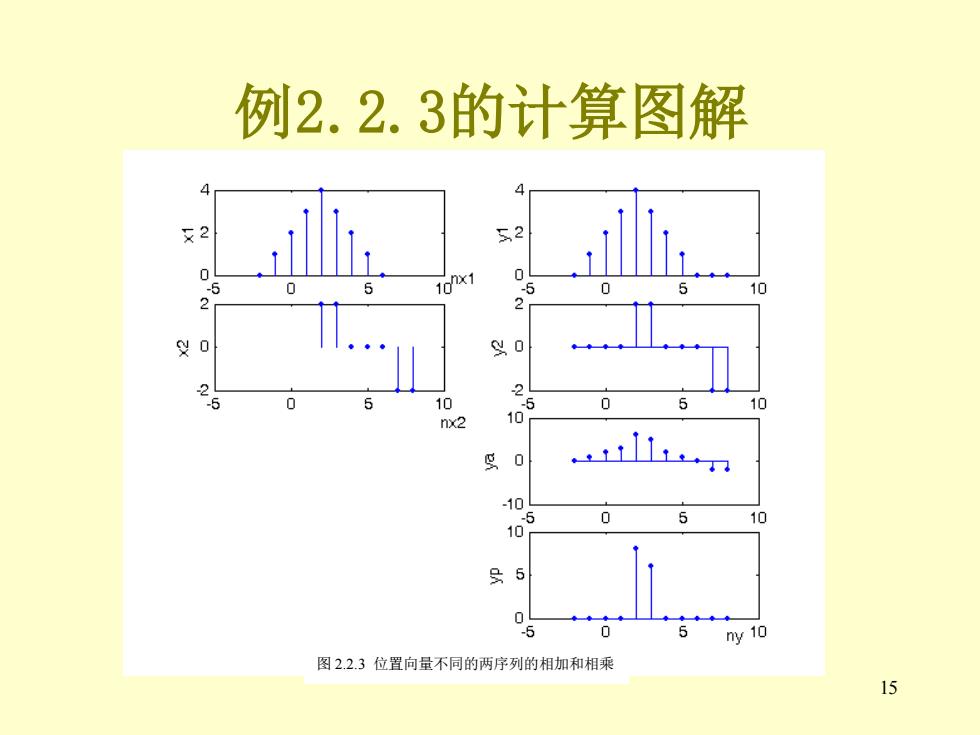
序列的相加和相乘运算 例2.2.3:x1=[0,1,2,3,4,3,2,1,0]n1=-2:6; x2=[2,2,0,0,0,-2,-2];n2=2:8 则 ny=-2:8; y1=[0,1,2,3,4,3,2,1,0,0,0] y2=[0,0,0,0,2,2,0,0,0,-2,-2]; yadd-y1+y2=[0,1,2,3,6,5,2,1,0,-2,-2] ymult=-y1.*y2=[0,0,0,0,6,9,0,0,0,0,0]
14 例2.2.3:x1=[0,1,2,3,4,3,2,1,0]; n1=-2:6; x2=[2,2,0,0,0,-2,-2]; n2=2:8 则 ny=-2:8; y1=[0,1,2,3,4,3,2,1,0,0,0]; y2= [0,0,0,0,2,2,0,0,0,-2,-2]; yadd=y1+y2=[0,1,2,3,6,5,2,1,0,-2,-2] ymult=y1.*y2=[0,0,0,0,6,9,0,0,0,0,0] 序列的相加和相乘运算
例2.2.3的计算图解 反2 10x 0 2 10 nx2 10 10 10 ny 10 图2.2.3位置向量不同的两序列的相加和相乘 15
15 例2.2.3的计算图解 图 2.2.3 位置向量不同的两序列的相加和相乘