
有限长序列DFT与DTFT关系Zx[k]-eiknX(ej)= DTFT(x[k]) =k=00-2元mlN-1AX[m]=Zx[k]-e,m=0,1,2....,N-1m=0X[m]=DFT(x[k])= X(ejn)m=0,1,2,..N-10=2元,有限长序列x[K]离散傅里叶变换X[m]是其离散时间傅里叶变换X(ej2)在一个周期[0,2元)的等间隔取样DFT与DFS关系2元mk[K]=X[m]-eN=x[k].R,[k]NZN-12元X[m=x(k]-e=X[m] R[m]k=0DFT可以看成是截取DFS的主值区间构成的变换对例:x[K]=8(k),0<k≤N-1,求N点DFTNN-x[kwm-[kjWmkXm=2k=0=1;0≤m≤N-12元),0≤≤N-1,求点DFT例:x[k]=cos(N一学ex[k]=N/2m=1N-1X[m]=10其它
有限长序列 DFT 与 DTFT 关系 =− = = k k X e x k x k e j -j ( ) DTFT{ [ ]} [ ] [ ] [ ] , 0,1,2, , 1 2 -j 1 0 = = − − = X m x k e m N mk N N m [ ] DFT{ [ ]} ( ) 2 , 0,1,2, , 1 j = = = − = X m x k X e m N m N 有限长序列 x[k]离散傅里叶变换 X[m]是其离散时间傅里叶变换 X(ej )在一个周期[0,2 )的等间隔取样 DFT 与 DFS 关系 [ ] [ ] ~ [ ] 1 [ ] 2 j 1 0 X m e x k R k N x k N mk N N m = = − = [ ] [ ] ~ [ ] [ ] 2 -j 1 0 X m x k e X m RN m km N N k = = − = DFT 可以看成是截取 DFS 的主值区间构成的变换对 例: x[k] =(k), 0 k N −1,求N点DFT mk N N k mk N N k X[m] x[k]W [k]W 1 0 1 0 − = − = = = =1; 0 m N −1 ), 0 1, DFT 2 例: [ ] cos( k k N 求N点 N x k = − ) 2 2 ( 1 [ ] ( 1) 2 j 2 j N k N k N e N e N N x k − = + = − = 0 其它 / 2 1, 1 [ ] N m N X m

例:求有限长4点序列 x[K]=(1,1,-1,1) 的 DFTN-!Ex[kjWmX[m]=DFT(x[k])=K=0X[0] = x[0] + x[1] + x[2] + x[3] = 2X[1] = x[0] +x[1]W] + x[2]W? +x[3]W? = 2X[2] = x[0]+x[1]W? + x[2]W4 + x[3]W = -2X[3] = x[0] + x[1]W? +x[2]W° +x[3]W° = 2如果序列后补零,其DFT有何变化?x,[K] = (1,1,1,1,0,0,0,0)2.1.3DFT矩阵表示有限长4点序列DFT矩阵表示[X[0]][wwowowTx[0]woW.w.w!x[1][1]w!X[2]W?Wtw?x[2] woW?wsw? x[3][X[3]][X[0]111-2112-1X[]1-jj1-1-1X[2]1I-2-1[X[3]1-1-i12X[m]=(2, 2, -2, 2),m=0,1,2,3DFT矩阵形式为X=Dx其中X-[X[0] X[]] .. X[N-]x=-[[0] [] x[N-]
例: 求有限长 4 点序列 x[k] ={1,1,−1,1} 的 DFT mk N N k X[m] DFT(x[k]) x[k]W 1 0 − = = = X[0] = x[0]+ x[1]+ x[2]+ x[3] = 2 [1] [0] [1] [2] [3] 2 3 4 2 4 1 X = x + x W4 + x W + x W = [2] [0] [1] [2] [3] 2 6 4 4 4 2 X = x + x W4 + x W + x W = − [3] [0] [1] [2] [3] 2 9 4 6 4 3 X = x + x W4 + x W + x W = 如果序列后补零,其 DFT 有何变化? [ ] {1,1, 1,1,0,0,0,0} x1 k = − 2.1.3 DFT 矩阵表示 有限长 4 点序列 DFT 矩阵表示 = [3] [2] [1] [0] [3] [2] [1] [0] 9 4 6 4 3 4 0 4 6 4 4 4 2 4 0 4 3 4 2 4 1 4 0 4 0 4 0 4 0 4 0 4 x x x x W W W W W W W W W W W W W W W W X X X X − = − − − − − − − = 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 [3] [2] [1] [0] j j j j X X X X X[m]={2,2,-2,2}, m=0,1,2,3 DFT 矩阵形式为 X = DN x 其中 [0] [1] [ 1] , T X = X X X N − [0] [1] [ 1] , T x = x x x N −

111WN-IW?W1-Wa(N-)W?wtDx =1...::....WN-Wa(w-)W(N-I)x(N-I)1IDFT矩阵形式为x=D-X[11111W-(N-I)wsWv?1Wr2W(N-1)Wr4D-=11........:.W(N-1)W-2(N-I)-(N-1)x(N-1)1W1D-LD'NNdftmtx(N)函数产生NXN的DFT矩阵DNconi(dftmtx(N)/N函数产生NXN的IDFT矩阵DN-1四、利用MATLAB计算DFTfft(x)fft(x,N)ifft(x)ifft(x,N)fft(x)计算M点的DFT。M是序列x的长度。fft(x,N)计算N点的DFT。M>N,将原序列裁为N点计算N点的DFTM<N,将原序列补零至N点,然后计算N点DFT。x[k]=cos(2mrk/ N),N=16,r=4利用MATLAB计算16点序列x[k]的512点DFTk = 0:15; L= 0:511;f=cos(2*pi*k*4./16);F = fft(f),plot(k/16,abs(F),o');hold onFE =fft(f,512);plot(L/512,abs(FE)
= − − − − − − 1 2( 1) ( 1) ( 1) 2 4 2( 1) 1 2 1 1 1 1 1 1 1 1 1 N N N N N N N N N N N N N N N N W W W W W W W W W D IDFT 矩阵形式为 x D X −1 = N = − − − − − − − − − − − − − − − ( 1) 2( 1) ( 1) ( 1) 2 4 2( 1) 1 2 ( 1) 1 1 1 1 1 1 1 1 1 N N N N N N N N N N N N N N N N W W W W W W W W W D − N = N N D D 1 1 dftmtx(N)函数产生 N×N 的 DFT 矩阵 DN conj(dftmtx(N))/N 函数产生 N×N 的 IDFT 矩阵 DN-1 四、利用 MATLAB 计算 DFT fft(x) fft(x,N) ifft(x) ifft(x,N) fft(x) 计算 M 点的 DFT。M 是序列 x 的长度。 fft(x,N) 计算 N 点的 DFT。 M>N,将原序列裁为 N 点计算 N 点的 DFT; M<N,将原序列补零至 N 点,然后计算 N 点 DFT。 x[k] = cos(2rk / N), N =16, r = 4 利用 MATLAB 计算 16 点序列 x[k]的 512 点 DFT k = 0:15; L = 0:511; f = cos(2*pi*k*4./16); F = fft(f); plot(k/16,abs(F),'o'); hold on FE = fft(f,512); plot(L/512,abs(FE))
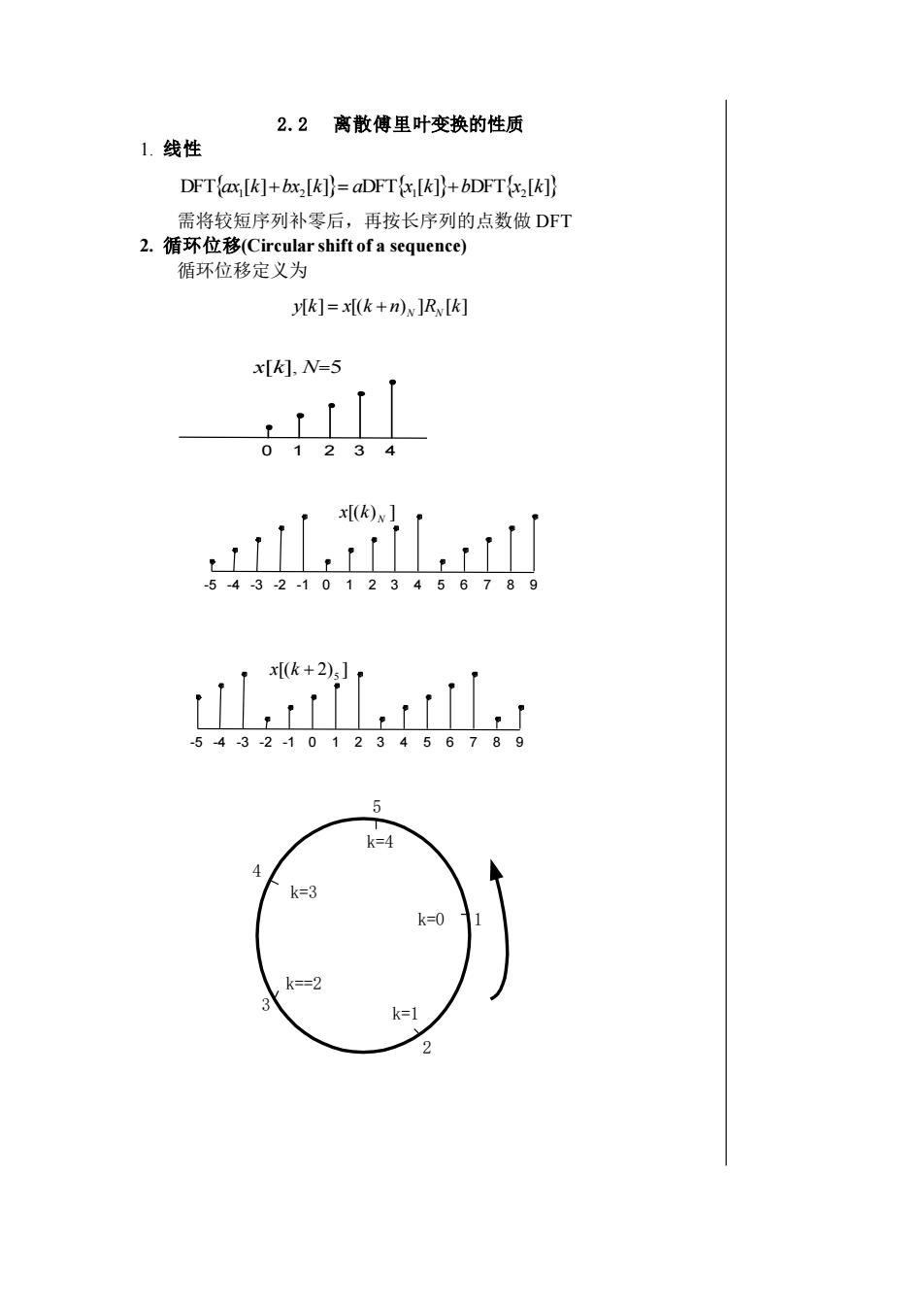
2.2离散傅里叶变换的性质1.线性DFT(ax[K]+ bx,[K]= aDFT (x[K])+ bDFT([K]需将较短序列补零后,再按长序列的点数做DFT2.循环位移(Circularshiftofasequence)循环位移定义为J[k]=x[(k +n)]R[k]x[k], N=52LOk=4k=3k=0k==2k=12
2.2 离散傅里叶变换的性质 1. 线性 DFTax1 [k]+bx2 [k]= aDFTx1 [k]+bDFTx2 [k] 需将较短序列补零后,再按长序列的点数做 DFT 2. 循环位移(Circular shift of a sequence) 循环位移定义为 y[k] x[(k n) ]R [k] = + N N x[k], N=5 0 1 2 3 4 [( ) ] N x k -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 [( 2) ] + 5 x k -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 1 5 4 3 2 k=0 k==2 k=1 k=4 k=3
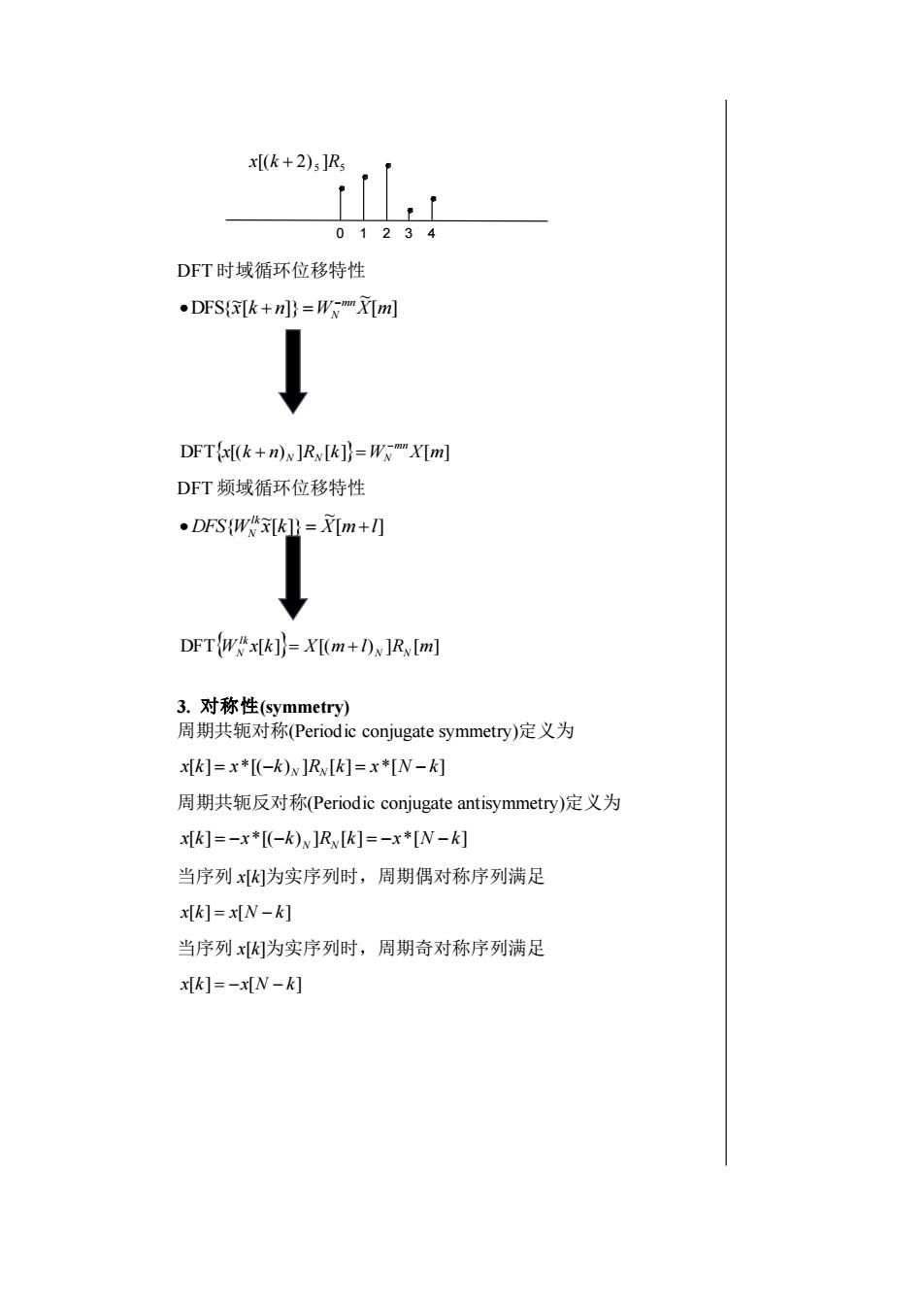
x[(k+2)sJR0123DFT时域循环位移特性.DFS([k+n]) =W-X[m]DFT(x[(k +n)]R[K])=W-""X[m]DFT频域循环位移特性.DFS(Wx[k])=X[m+]]DFT(w*x[K]= X[(m+ I) ]JR[m]3.对称性(symmetry)周期共轭对称(Periodicconjugatesymmetry)定义为x[k]= x*[(-k)]R[K]= x*[N-k]周期共轭反对称(Periodicconjugateantisymmetry)定义为x[k]=-x*[(-k)~]R[k]= -x*[N -k]当序列x[K]为实序列时,周期偶对称序列满足x[k]=x[N-k]当序列x[K]为实序列时,周期奇对称序列满足x[k]=-x[N -k]
DFT 时域循环位移特性 [ ] ~ [ ]} ~ DFS{x k n W X m mn N − • + = DFTx[(k n) ]R [k] W X[m] mn N N N − + = DFT 频域循环位移特性 [ ] ~ [ ]} ~ DFS{W x k X m l lk • N = + DFTW x[k] X[(m l) ]R [m] N N lk N = + 3. 对称性(symmetry) 周期共轭对称(Periodic conjugate symmetry)定义为 x[k] x*[( k) ]R [k] x*[N k] = − N N = − 周期共轭反对称(Periodic conjugate antisymmetry)定义为 x[k] x*[( k) ]R [k] x*[N k] = − − N N = − − 当序列 x[k]为实序列时,周期偶对称序列满足 x[k] = x[N − k] 当序列 x[k]为实序列时,周期奇对称序列满足 x[k] = −x[N − k] 5 5 x[(k + 2) ]R 0 1 2 3 4