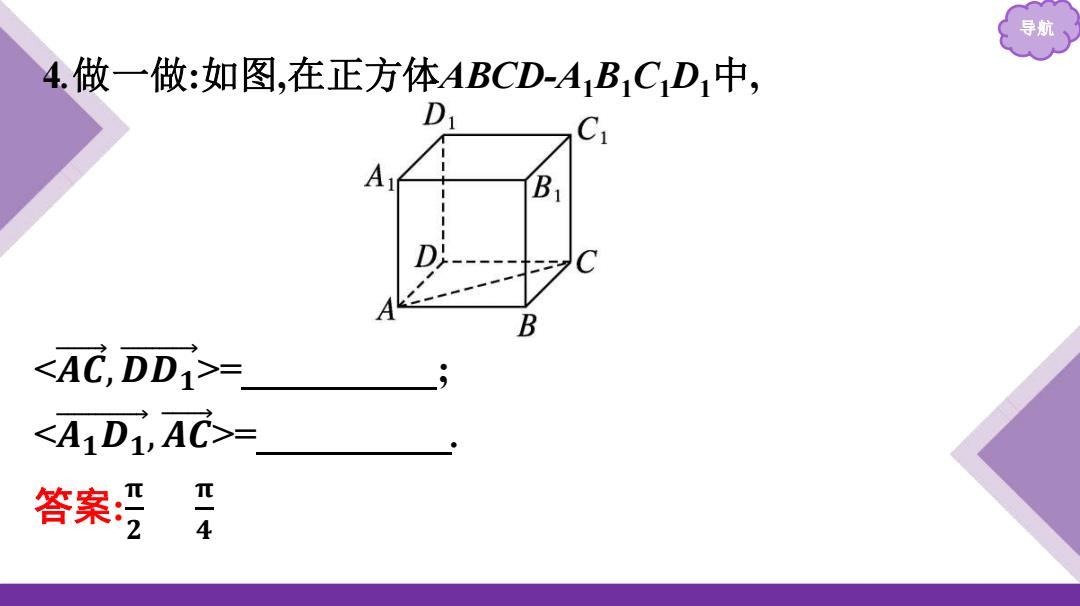
导航 4.做一做:如图,在正方体ABCD-A1BCD1中, D A B D C B <AC,DD> <A Di AC>= 答案开
导航 4 .做一做 :如图 ,在正方体ABCD -A 1 B 1 C1 D 1 中, <𝑨 𝑪 , 𝑫 𝑫 𝟏 >= ; <𝑨𝟏𝑫𝟏 ,𝑨 𝑪 >= . 答案:𝛑𝟐 𝛑𝟒

导航 二、空间向量的数量积 【问题思考】 1.向量a在向量b上的投影是向量还是实数? 提示:向量 2.平面向量的数量积的概念与性质,能否将它们从平面推广到 空间中? 提示:能
导航 二、空间向量的数量积 【问题思考】 1.向量a在向量b上的投影是向量还是实数? 提示:向量. 2.平面向量的数量积的概念与性质,能否将它们从平面推广到 空间中? 提示:能

3填空: ()定义:空间中,两个非零向量a与b的数量积(也称为内积)定 义为 (2)空间向量的数量积的性质 ①a⊥b曰ab= ②aa=a2= ③a-b allb ④(2a)b=2(ab). ⑤ab=(交换律) ⑥(a+b)c= (分配律)
导航 3.填空: (1)定义:空间中,两个非零向量a与b的数量积(也称为内积)定 义为 a·b=|a||b|cos<a,b> . (2)空间向量的数量积的性质 ①a⊥b⇔a·b= 0 . ②a·a=|a| 2= a 2 . ③|a·b| ≤ |a||b|. ④(λa)·b=λ(a·b). ⑤a·b= b·a (交换律). ⑥(a+b)·c= a·c+b·c (分配律)

导航 4.做一做:在正四面体O-ABC中,若其棱长为1,则AC. OB= 解析:AC.0B=(oC-0本0B=0C.OB-0A. 0B=1×1×c0s60°-1×1×c0s60°=0. 答案:0
导航 4.做一做:在正四面体 O-ABC 中,若其棱长为 1,则𝑨 𝑪 · 𝑶 𝑩 = . 解析:𝑨 𝑪 ·𝑶 𝑩 =(𝑶 𝑪 − 𝑶 𝑨 )·𝑶 𝑩 = 𝑶 𝑪 ·𝑶 𝑩 − 𝑶 𝑨 · 𝑶 𝑩 =1×1×cos 60°-1×1×cos 60°=0. 答案:0

导航 思考辨析】 判断正误(正确的画“V”,错误的画“X) (1)两个向量的夹角的范围是0,).( (2)对于非零向量a,b,必有<a,b>=<-a,-b>.( (3)la-b=a-b (4)(ab)c=a(bc.( (⑤)若ab=bc,则a=c.( (6)(a+b)2=a2+2ab+b2.(
导航 【思考辨析】 判断正误.(正确的画“√”,错误的画“×”) (1)两个向量的夹角的范围是[0,π).( × ) (2)对于非零向量a,b,必有<a,b>=<-a,-b>.( √ ) (3)|a·b|=|a|·|b|.( × ) (4)(a·b)·c=a·(b·c).( × ) (5)若a·b=b·c,则a=c.( × ) (6)(a+b)2=a 2+2a·b+b 2 .( √ )