华东理工大学：《线性代数》课程电子教案（PPT课件）第一章 矩阵

设矩陈4-(g72)n-6》 且3B+2X=2A,求X. 解：由矩阵数乘减法运算可知 X-24-3B-A-3B 2 4 区回

3 2 2 , . , 0 4 2 2 4 2 , 3 1 2 1 7 5 1: B X A X A B 且 求 例 设矩阵 + =         − − =         − = A B A B X 2 3 2 2 3 : , = − − = 解 由矩阵数乘减法运算可知         − − = 3 7 5 2 1 8         − − −        − = 0 4 2 2 4 2 2 3 3 1 2 1 7 5

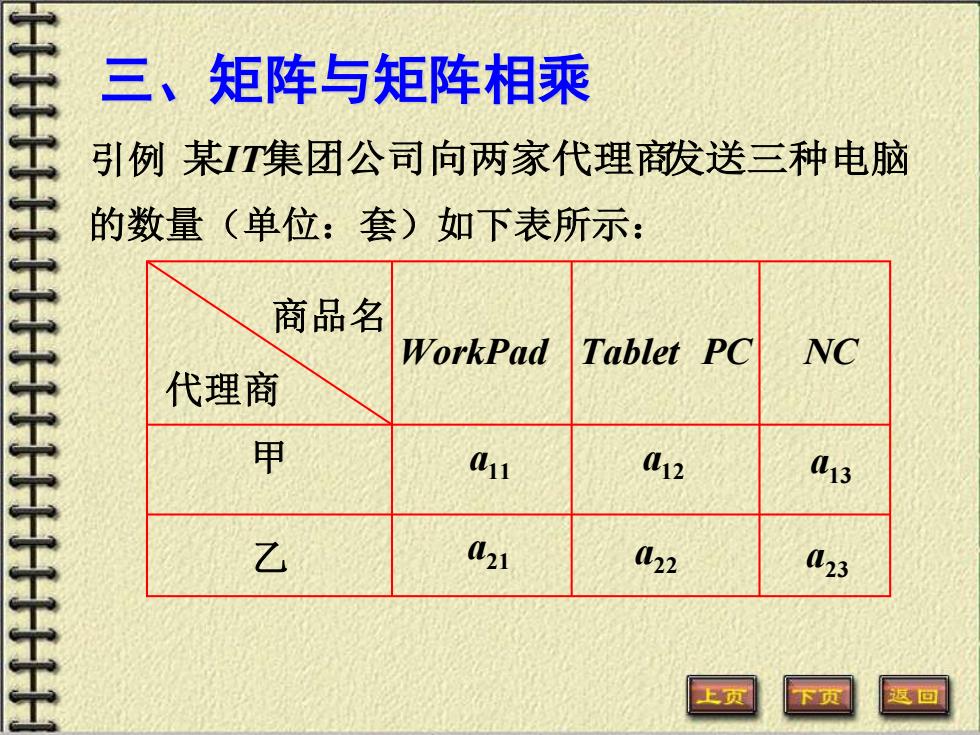
三、矩阵与矩阵相乘 引例某IT集团公司向两家代理酸送三种电脑 的数量（单位：套）如下表所示： 商品名 WorkPad Tablet PC NC 代理商 甲 41 12 013 乙 421 22 23

三、矩阵与矩阵相乘 引例 某IT集团公司向两家代理商发送三种电脑 的数量（单位：套）如下表所示： 商品名 代理商 WorkPad Tablet PC NC 甲 乙 11 a 12 a a13 a21 a22 a23

表格中的数据对应矩阵： 12 13 421 L22 23 这三种电脑的单价及单件重量也可以列成矩阵： b2 B= b21 b22 b31 b32 其中，b,表示第种电脑的单价，b2表示第种电脑 的单件重量(i=1,2,3) 试问：该T公司向代理商乙所发送电脑的总 重量是多少？

表格中的数据对应矩阵：       = 21 22 23 11 12 13 a a a a a a A 这三种电脑的单价及单件重量也可以列成矩阵：           = 31 32 21 22 11 12 b b b b b b B ( 1,2,3). 1 2 i = b i b i i i 的单件重量 其中， 表示第 种电脑的单价， 表示第 种电脑 重量是多少？ 试问：该IT公司向代理商乙所发送电脑的总

显然，由A、B的意义即 b11 012 B= b21 22 b31 可知21b12+22b22+a23b32即为所求 于是，可得该公司向两家代理商所发送电脑的 总价值与总重量矩阵： C= 41b1+a12b21+413b31a1ib12+a12b2+a13b2 La2ibi1+a22b21+a23b31a21b12+a22b22+a23b32」 我们可以认为矩阵C是矩阵A、B的“乘积”. 于是，有

      = 21 22 23 11 12 13 a a a a a a A           = 31 32 21 22 11 12 b b b b b b B 显然，由A、B的意义即 . 可知a21b12 + a22b22 + a23b32即为所求 于是，可得该公司向两家代理商所发送电脑的 总价值与总重量矩阵：       + + + + + + + + = 2 1 1 1 2 2 2 1 2 3 3 1 2 1 1 2 2 2 2 2 2 3 3 2 1 1 1 1 1 2 2 1 1 3 3 1 1 1 1 2 1 2 2 2 1 3 3 2 a b a b a b a b a b a b a b a b a b a b a b a b C 我们可以认为矩阵C是矩阵A、B的“乘积”. 于是，有

1、定义 设A=(a,)是一个m×s矩阵，B=(b,)是一个 s×n矩阵，那么规定矩阵A与矩阵B的乘积 是一个mxn矩阵C=(cn),其中 Co-anbu +anb+..+ab,=Eanby (i=1,2,…m5j=1,2,…,n) 并把此乘积记作Cmxn=Anx,B,xn 回

１、定义 = + + + =  = s k i j ai b j ai b j ai sbsj ai k bkj c 1 1 1 2 2  (i = 1,2, m; j = 1,2,  ,n), 并把此乘积记作 . Cmn = Ams Bsn 设 是一个 矩阵， 是一个 矩阵，那么规定矩阵 与矩阵 的乘积 是一个 矩阵 ，其中 ( ) A = aij m s ( ) B = bij sn mn ( )ij C = c A B