
3求由摆线tsn,1e0,2z与x轴 y=a(1-cost)' 所围图形的面积 y↑ 2 A 2πa 解S(A)=∫a(l-cost)a(t-sint)dt a[(1-cost)'dt=3za
2 2 2 2 0 a t t a (1 cos ) d 3 . 解 2 0 S A a t a t t t ( ) (1 cos )[ ( sin )] d 所围图形的面积. a 2a x y O 2a A 例3 与 x 轴 ( sin ) , [0, 2 ] (1 cos ) x a t t t y a t 求由摆线

3メ 例4求椭圆 =1的面积 解椭圆的参数方程 - 由对称性知总面积等于4倍第一象限部分面积. ysintd(acost) =4 abf:sin2h=元ab
例 4 求椭圆 1 2 2 2 2 b y a x 的面积. y b t x a t sin cos a A ydx 0 4 0 2 4 bsintd(acost) ab tdt 2 0 2 4 sin ab. 解 椭圆的参数方程 由对称性知总面积等于4倍第一象限部分面积.
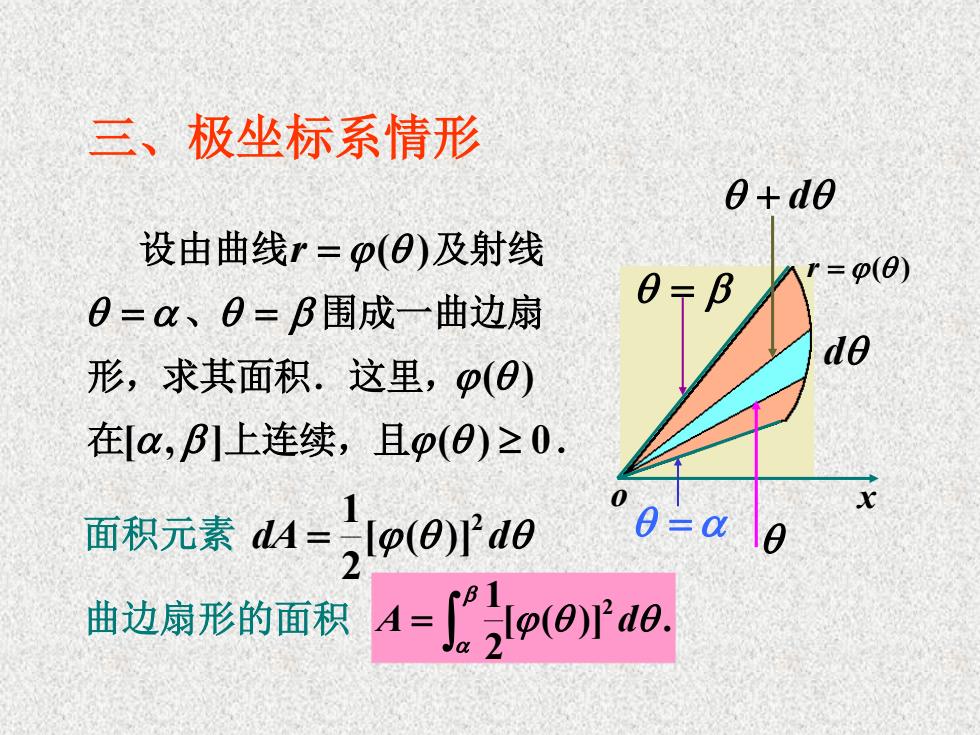
三、极坐标系情形 0+d0 设由曲线r=p(O)及射线 0=a、0=B围成一曲边扇 8=B r=p(8) 形,求其面积.这里,p(O) d0 在[a,B]上连续,且p(0)≥0. 面积元素M=lo(0)ra0 0=a 曲边扇形的面积A=o(0'd0
设由曲线r ( )及射线 、 围成一曲边扇 形,求其面积.这里,( ) 在[, ]上连续,且( ) 0. o x d d dA d 2 [ ( )] 2 1 [ ( )] . 2 1 2 A d 三、极坐标系情形 r ( ) 曲边扇形的面积 面积元素

例题解析 例4求心脏线r=(1+cos)所围平面图形的面积. 解 r=a(1+cose) S(-a(1+cos0)Fd0 =a20(1+cos02d6 2a x 3 πa2. 2
例4 求心脏线 r a (1 cos ) . 所围平面图形的面积 解 2π 2 0 1 ( ) [ (1 cos )] d 2 S A a 3 2 π . 2 a π 2 2 0 a (1 cos ) d O x y a 2a r a (1 cos ) 例题解析

例5求双纽线r2=a2cos20所围平面图形的面积. 解因为r2≥0,所以0的取值 范困是1子与子到 由图形的对称性, s0=4广acs20a6 -a'sin201=a
例5 2 2 求双纽线 r a cos2 . 所围平面图形的面积 由图形的对称性, π 2 4 0 1 ( ) 4 cos 2 d 2 S A a 解 2 因为r 0, 所以 的取值 π π 3π 5π [ , ] [ , ]. 4 4 4 4 范围是 与 π 2 2 4 0 a a sin2 . a/2 a O y x