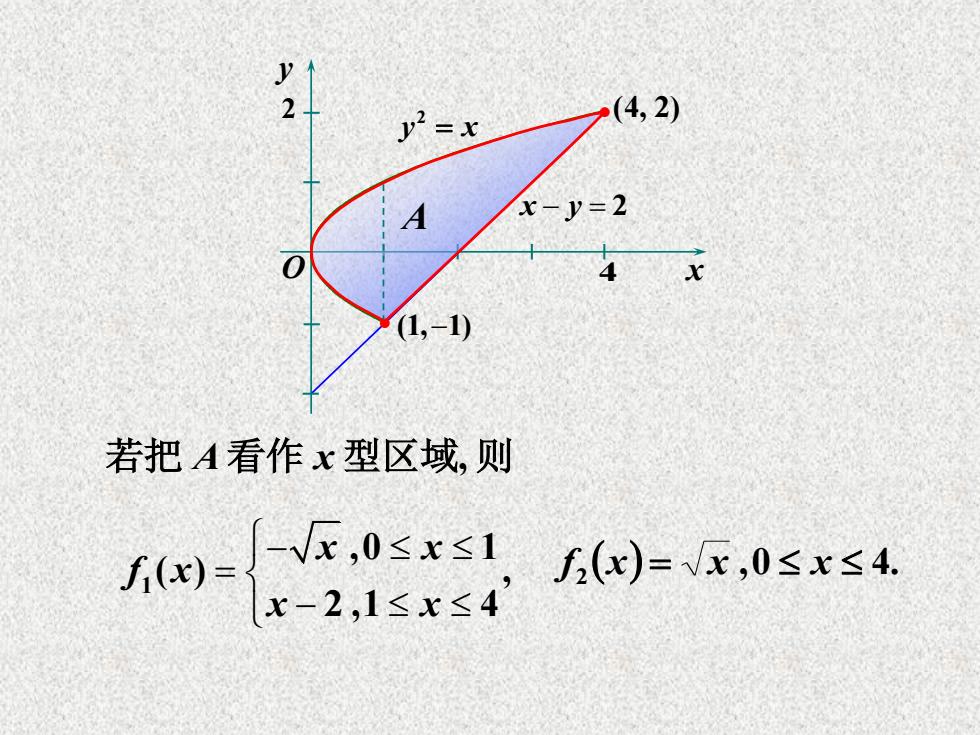
y 2 y2=x (4,2) x-y=2 (1,-10 若把A看作x型区域,则 f四=x,0sxs1 f2(x)=Nx,0≤x≤4. x-2,1≤x≤4
1 ,0 1 ( ) , 2 ,1 4 x x f x x x ,0 4. f 2 x x x 若把 A x 看作 型区域, 则 2 4 y x 2 (4, 2) x y O x y 2 (1, 1) A

由于f分段定义,A分为二图形A和A, s4t(mjar号 s4)=(Nc-(x-2列 号可甘号 3 则 SA0=s4)+(4)=3+3 414 39 2 2
4 2 1 S A x x x ( ) ( 2) d 1 1 3 2 1 0 0 4 4 ( ) ( ) d . 3 3 S A x x x x 1 1 2 由于 f A A A 分段定义, , 分为二图形 和 1 2 4 14 3 9 ( ) ( ) ( ) . 3 3 2 2 S A S A S A 4 2 3 2 1 2 14 3 2 . 3 2 3 2 x x x 则

若把A看作为y型区域,则 g1Uy)=y2(-1≤y≤2),g20y)=y+2(-1≤y≤2). s4=0y+2)-y21 +2房号 显然,由于g1),g20)不是分段定义的函数,比较 容易计算
. 2 9 1 2 3 1 2 2 1 2 3 y y y 显然,由于 g1 (y), g2 (y) 不是分段定义的函数,比较 若把 A y 看作为 型区域,则 2 1 2 g y y y g y y y ( ) ( 1 2), ( ) 2 ( 1 2). 2 2 1 S A y y y ( ) [( 2) ]d 容易计算

•参数方程 设曲线C是由参数方程x=x(t),y=y(t),t∈[a,B]给出, 在[a,β]上y(t)连续,x(t)连续可微且x(t)≠O, 记a=x(a),b=x(B),(a<b或b<a), 则由曲线C及直线x=a,x=b和x轴所围图形面积公式为 4-(os(
设曲线C是由参数方程 x x(t), y y(t),t [,]给出, [ , ] ( ) ( ) ( ) 0, ' 在 上y t 连续,x t 连续可微且x t 记a x(),b x(),(a b或b a), 则由曲线C及直线x a, x b和x轴所围图形面积公式为 ( ) ( ) . ' A y t x t dt •参数方程

二参数方程 如果曲边梯形的曲边为参数方程 Jx=p(t) [y=v(t) 由边梯形的面积4y0p'0)d (其中t,和t,对应曲线起点与终点的参数值) 在[t1,t2】(或[t2,t1)上x=p(t)具有连续导数, y=业(t)连续
如果曲边梯形的曲边为参数方程 ( ) ( ) y t x t 2 1 ( ) ( ) . t t A t t dt (其中 1 t 和 2 t 对应曲线起点与终点的参数值) 在[ 1 t , 2 t ](或[ 2 t , 1 t ])上x (t)具有连续导数, y (t)连续. 曲边梯形的面积 •二 参数方程