
问题1级数(1)的收敛域如何求得? 问题2级数(1)的收敛域有何特点? anr”=a+ax+a,r2+.+a,r"+ (1) n=0 ∑la|=la+la+.+la,x+. (2) 若级数(2)收敛,则级数()必收敛,称(1)绝对收敛; 若级数(1)收敛,则级数(2)未必收敛; 若级数(2)依比值法或根值法判定发散,则级数(1)必 发散
问题1 级数(1)的收敛域如何求得? 问题2 级数(1)的收敛域有何特点? 若级数(2)收敛,则级数(1)必收敛,称(1)绝对收敛; 若级数(1)收敛,则级数(2)未必收敛; 若级数(2)依比值法或根值法判定发散,则级数(1)必 发散
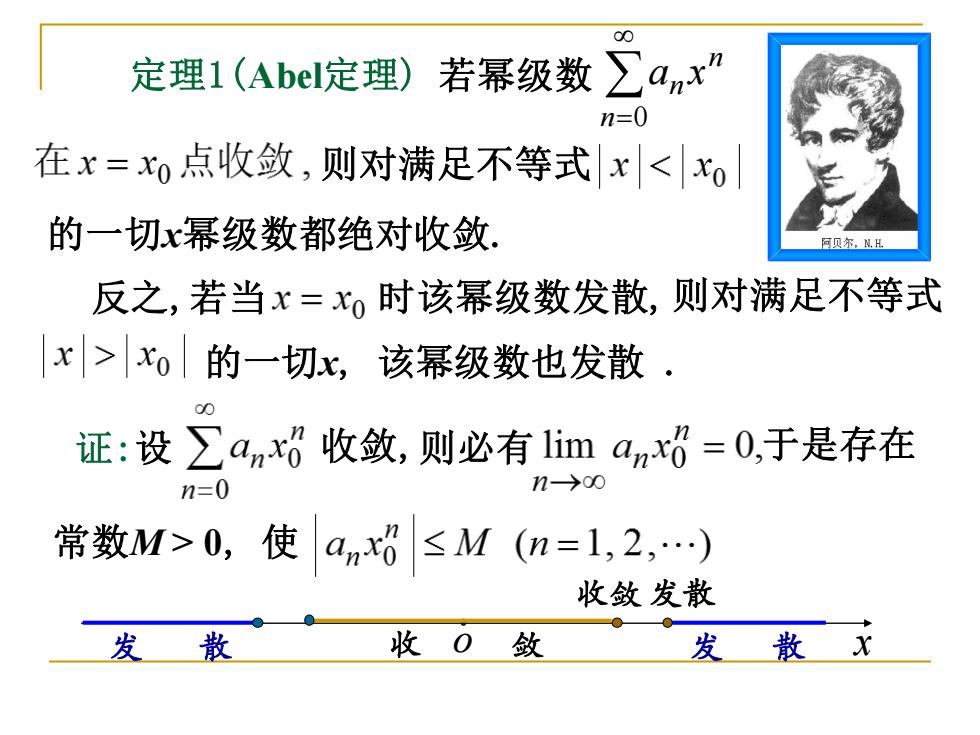
●人● 定理1(Abel定理)若幂级数 ∑anx” n=0 在x=xo点收敛,则对满足不等式x<xo 的一切x幂级数都绝对收敛, 阿贝尔,H 反之,若当x=xo时该幂级数发散,则对满足不等式 x>xo的一切x,该幂级数也发散 证:设∑anx收敛,则必有1iman=0,于是存在 n=0 n→00 常数M>0,使anx≤M(n=1,2,.) 收敛发散 发 散 收0敛 发散X
发 散 收 o 敛 发 散 x 收敛 发散 定理1(Abel定理) 若幂级数 n=0 n n a x 则对满足不等式 的一切x幂级数都绝对收敛. 反之,若当 的一切x, 该幂级数也发散 . 时该幂级数发散,则对满足不等式 证:设 收敛,则必有 于是存在 常数M > 0, 使