
§2图解法及单纯型法解题思路 (2)对每个不等式(约束条件),先取其等式在坐标系中作直 线,然后确定不等式所决定的半平面。 400 300 3001 200 X1+x2=300 200 2x1+x2=400 100 100 100 200 300 2X1+x2≤400 16020ù 300 X1+x2≤300 11
管 理 运 筹 学 11 §2 图解法及单纯型法解题思路 (2)对每个不等式(约束条件),先取其等式在坐标系中作直 线,然后确定不等式所决定的半平面。 100 200 300 100 200 300 x1+x2≤300 x1+x2=300 100 2x 100 200 1+x2≤400 2x1+x2=400 300 200 300 400

§2图解法及单纯型法解题思路 (3)把五个图合并成一个图,取各约束条件的公共部分,如 图2-1所示。 x2=250 2x1+x2=400 300 X2=250 200 100/ X2≤250 X1+x2=300 100200300 X2=-0 X 4一X1=0 图2-1 非 12
管 理 运 筹 学 12 §2 图解法及单纯型法解题思路 (3)把五个图合并成一个图,取各约束条件的公共部分,如 图2-1所示。 100 100 x2≤250 x2=250 200 300 200 300 x1 x2 x2=0 x1=0 x2=250 x1+x2=300 2x1+x2=400 图2-1
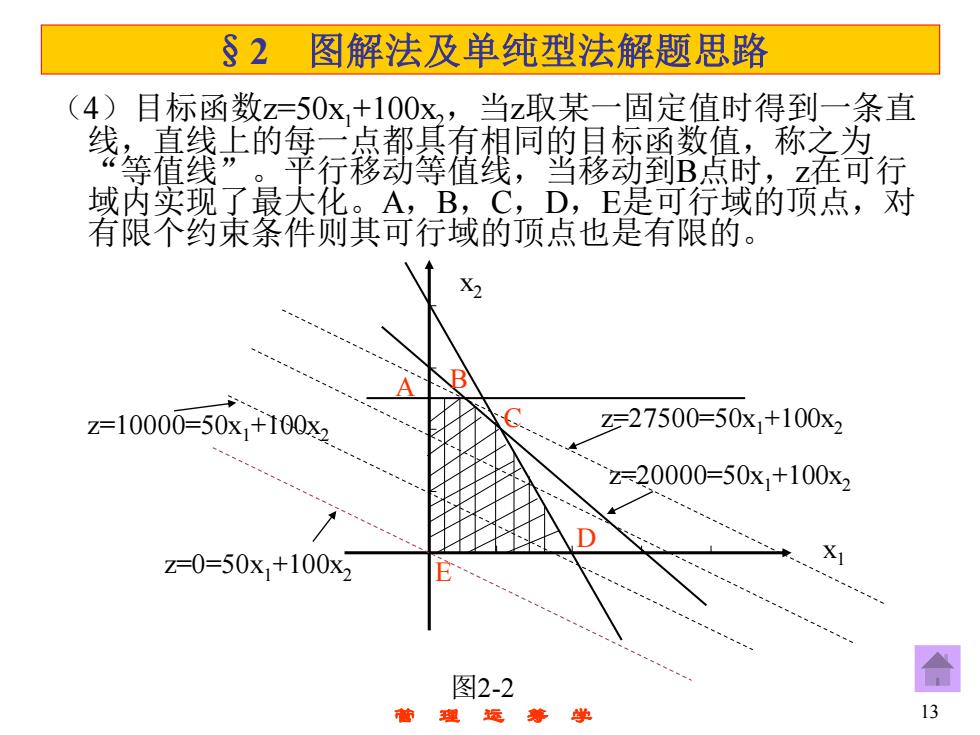
§2 图解法及单纯型法解题思路 (4) 目标函数z=50x,+100x,当z取某一固定值时得到一条直 线,真线上的每,二点都具有相同的标函数值,称之为 等值线” 行移动等值线,当移动到B点时,Z在可行 域内实现了最大化。A,B,C,D,E是可行域的顶点,对 有限个约束条件则其可行域的顶点也是有限的。 z=10000=50x1+I00x2 z=27500=50x1+100x2 z=20000=50x1+100x2 z=0=50x1+100x2 图2-2 13
管 理 运 筹 学 13 §2 图解法及单纯型法解题思路 (4)目标函数z=50x1+100x2,当z取某一固定值时得到一条直 线,直线上的每一点都具有相同的目标函数值,称之为 “等值线”。平行移动等值线,当移动到B点时,z在可行 域内实现了最大化。A,B,C,D,E是可行域的顶点,对 有限个约束条件则其可行域的顶点也是有限的。 x1 x2 z=20000=50x1+100x2 图2-2 z=27500=50x1+100x2 z=0=50x1+100x2 z=10000=50x1+100x2 C A B D E

§2 图解法及单纯型法解题思路 重要结论: -如果线性规划有最优解,则一定有一个可行域 的顶点对应一个最优解; 无穷多个最优解。若将例1中的目标函数变为 maxz=50x+50x2,则线段BC上的所有点都代表 了最优解: 无界解。即可行域的范围延伸到无穷远,目标 函数值可以无穷大或无穷小。一般来说,这说 明模型有错,忽略了一些必要的约束条件; 无可行解。若在例1的数学模型中再增加一个约 束条件4x+3x≥1200,则可行域为空域,不存在 满足约束条件的解,当然也就不存在最优解了。 14
管 理 运 筹 学 14 §2 图解法及单纯型法解题思路 • 重要结论: – 如果线性规划有最优解,则一定有一个可行域 的顶点对应一个最优解; – 无穷多个最优解。若将例1中的目标函数变为 max z=50x1+50x2,则线段BC上的所有点都代表 了最优解; – 无界解。即可行域的范围延伸到无穷远,目标 函数值可以无穷大或无穷小。一般来说,这说 明模型有错,忽略了一些必要的约束条件; – 无可行解。若在例1的数学模型中再增加一个约 束条件4x1+3x2≥1200,则可行域为空域,不存在 满足约束条件的解,当然也就不存在最优解了
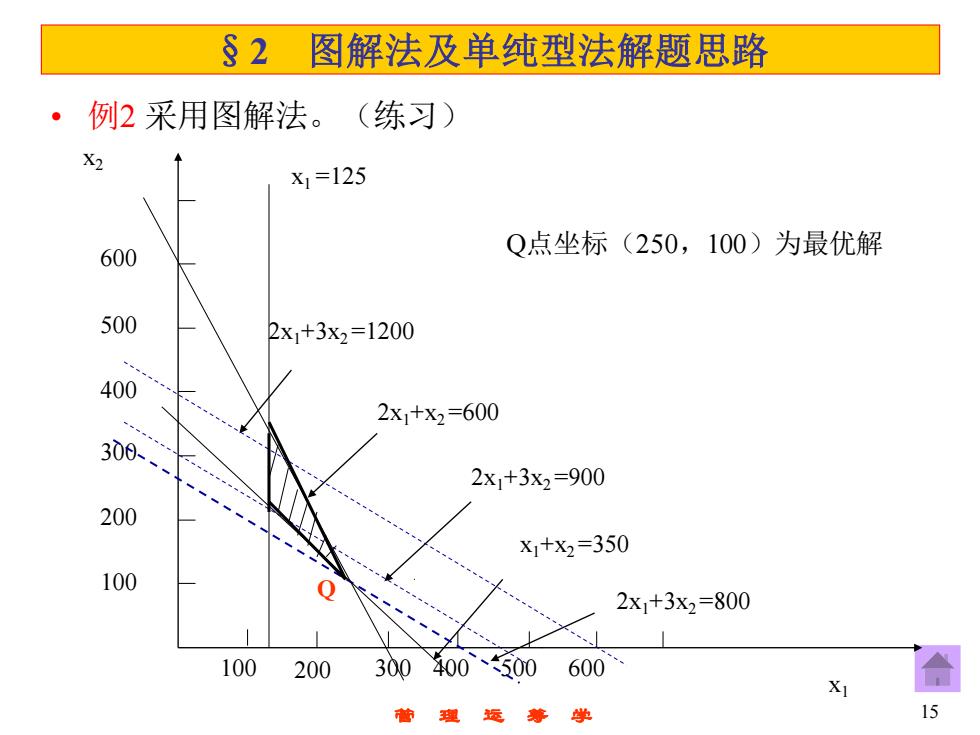
§2 图解法及单纯型法解题思路 例2采用图解法。(练习) X1=125 600 Q点坐标(250,100)为最优解 500 2X1+3x2=1200 400 2x1+X2=600 300、 2x1+3x2=900 200 X1+x2=350 100 2x1+3x2=800 100 200 300400500 600 15
管 理 运 筹 学 15 • 例2 采用图解法。(练习) 100 200 300 400 500 600 100 200 300 400 600 500 x1 =125 x1+x2 =350 2x1+3x2 =800 2x1+3x2 =900 2x1+x2 =600 2x1+3x2 =1200 x1 x2 Q §2 图解法及单纯型法解题思路 Q点坐标(250,100)为最优解