
§1线性规划问题的提出及其数学模型 决策变量:x1,原料A的购买量,x2:原料B购买量 目标函数: Min f=2x+3x2 约束条件: s.t. X1+X2≥350 Xj ≥125 2X1+X2≤600 X1,X2≥0 6
管 理 运 筹 学 6 §1 线性规划问题的提出及其数学模型 决策变量: x1:原料A的购买量,x2:原料B购买量 目标函数: Min f = 2x1 + 3 x2 约束条件: s.t. x1 + x2 ≥ 350 x1 ≥ 125 2 x1 + x2 ≤ 600 x1 , x2 ≥ 0

§1线性规划问题的提出及其数学模型 建模过程 1.理解要解决的问题,了解解题的目标和条件: 2定义决策变量(X1,X2,x),每一组值表 示一个方案; 3.用决策变量的线性函数形式写出目标函数,确定最 大化或最小化目标; 4.用一组决策变量的等式或不等式表示解决问题过程 中必须遵循的约束条件
管 理 运 筹 学 7 §1 线性规划问题的提出及其数学模型 • 建模过程 1.理解要解决的问题,了解解题的目标和条件; 2.定义决策变量( x1 ,x2 ,. ,xn ),每一组值表 示一个方案; 3.用决策变量的线性函数形式写出目标函数,确定最 大化或最小化目标; 4.用一组决策变量的等式或不等式表示解决问题过程 中必须遵循的约束条件

§1线性规划问题的提出及其数学模型 一般形式 决策变量设置: X1,X2,.’X 目标函数: Max (Min)Z=c1x1+c2 x2+.Cn Xn 约束条件: s.t. ++至8 amlX1+am2X2+.+amnX≤(=,≥)bm X1’X2,.,X≥0
管 理 运 筹 学 8 §1 线性规划问题的提出及其数学模型 • 一般形式 决策变量设置: x1, x2, . , xn 目标函数: Max (Min) z = c1 x1 + c2 x2 + . + cn xn 约束条件: s.t. a11 x1 + a12 x2 + . + a1n xn ≤ ( =, ≥ )b1 a21 x1 + a22 x2 + . + a2n xn ≤ ( =, ≥ )b2 . . am1 x1 + am2 x2 + . + amn xn ≤ ( =, ≥ )bm x1 ,x2 ,. ,xn ≥ 0
§2图解法及单纯型法解题思路 对于只有两个决 例1.目标函数: 策变量的线性规划问 Max z=50X1+100x2 题,可以在平面直角 约束条件: 坐标系上作图表示线 s.t. 性规划问题的有关概 X1+ X2≤300 (A) 2X1+ X≤ 400 (B) 念,并求解。 X≤250 (C) 下面通过例1详细 X1≥0 (D) 2≥0 (E) 讲解其方法: 得到最优解: X1=50, X2=250 最优目标值z=27500 9
管 理 运 筹 学 9 例1.目标函数: Max z = 50 x1 + 100 x2 约束条件: s.t. x1 + x2 ≤ 300 (A) 2 x1 + x2 ≤ 400 (B) x2 ≤ 250 (C) x1 ≥ 0 (D) x2 ≥ 0 (E) 得到最优解: x1 = 50, x2 = 250 最优目标值 z = 27500 §2 图解法及单纯型法解题思路 对于只有两个决 策变量的线性规划问 题,可以在平面直角 坐标系上作图表示线 性规划问题的有关概 念,并求解。 下面通过例1详细 讲解其方法:
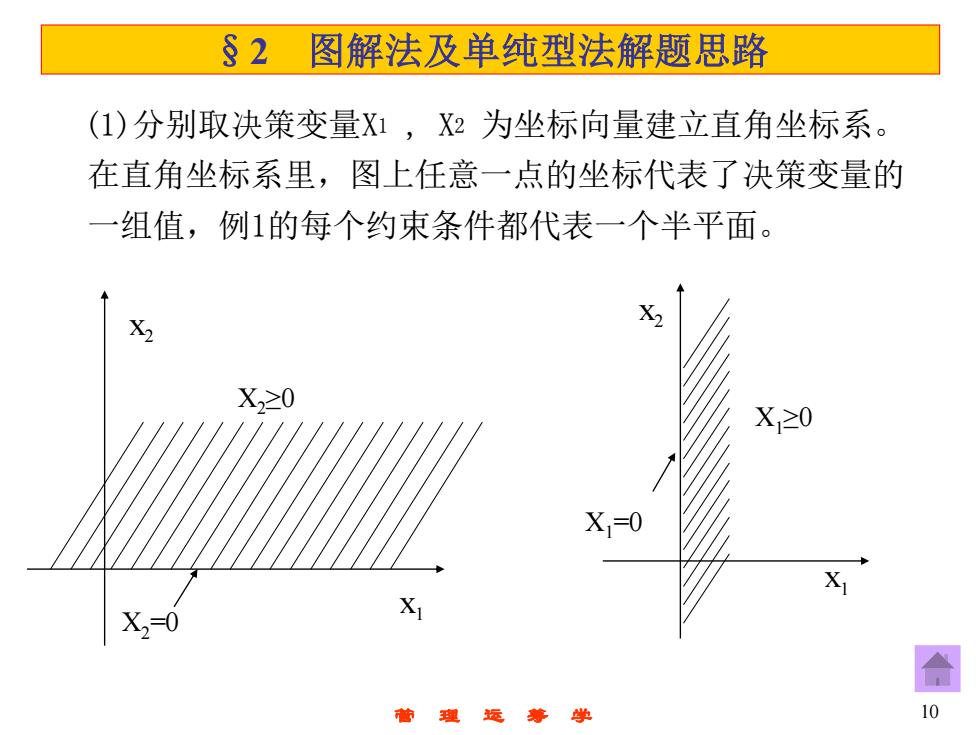
§2图解法及单纯型法解题思路 (1)分别取决策变量X1,X2为坐标向量建立直角坐标系。 在直角坐标系里,图上任意一点的坐标代表了决策变量的 一组值,例1的每个约束条件都代表一个半平面。 X X2≥0 X1≥0 X=0 X X2=0 X 10
管 理 运 筹 学 10 §2 图解法及单纯型法解题思路 (1)分别取决策变量X1 , X2 为坐标向量建立直角坐标系。 在直角坐标系里,图上任意一点的坐标代表了决策变量的 一组值,例1的每个约束条件都代表一个半平面。 x2 x1 X2≥0 X2=0 x2 x1 X1≥0 X1=0