海南大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵

数乘矩阵满足的运算规律： (设A、B为m×n矩阵，L,u为数) (1)(24)A=2(4)片 (2)(2+4)A=M+A; 3)2(A+B)=A+2B. 矩阵相加与数乘矩阵合起来，统称为矩阵的线性运算

(1)()A = (A); (2)( + )A = A+ A; (3) (A+ B) = A+ B. 数乘矩阵满足的运算规律： 矩阵相加与数乘矩阵合起来,统称为矩阵的线性运算. （设 A、B 为 mn 矩阵，  , 为数）

4.矩阵与矩阵相乘 定义：设A=(4n)是一个m×s矩阵，B=(bn)是一个 s×n矩阵，那末规定矩阵A与矩阵B的乘积 是一个m×n矩阵C=(c,),其中 0,=a,b+ab,++h,=2aA, (i=1,2,.m5j=1,2,.,n月 并把此乘积记作 C=AB

定义： = = + + + = s k ij ai b j ai b j aisbsj aikbkj c 1 1 1 2 2  (i = 1,2, m; j = 1,2,  ,n), 并把此乘积记作 C = AB. 4. 矩阵与矩阵相乘 ( )ij C = c 设 是一个 矩阵， 是一个 矩阵，那末规定矩阵 与矩阵 的乘积 是一个 矩阵 ，其中 ( ) A = aij m  s ( ) B = bij s  n m  n A B

之书动 例1： 例2： 0 3 4 (10-12 2 A= 1 -1130 B= 、05- 14 3 1 1 21 求AB

例１： 2 2 2 2 3 6 2 4 1 2 2 4         − −       − − C = 22       = − 16 − 32 8 16           − − − = 0 5 1 4 1 1 3 0 1 0 1 2 A               − − = 1 2 1 3 1 1 1 2 1 0 3 4 B 例2： ? 求AB

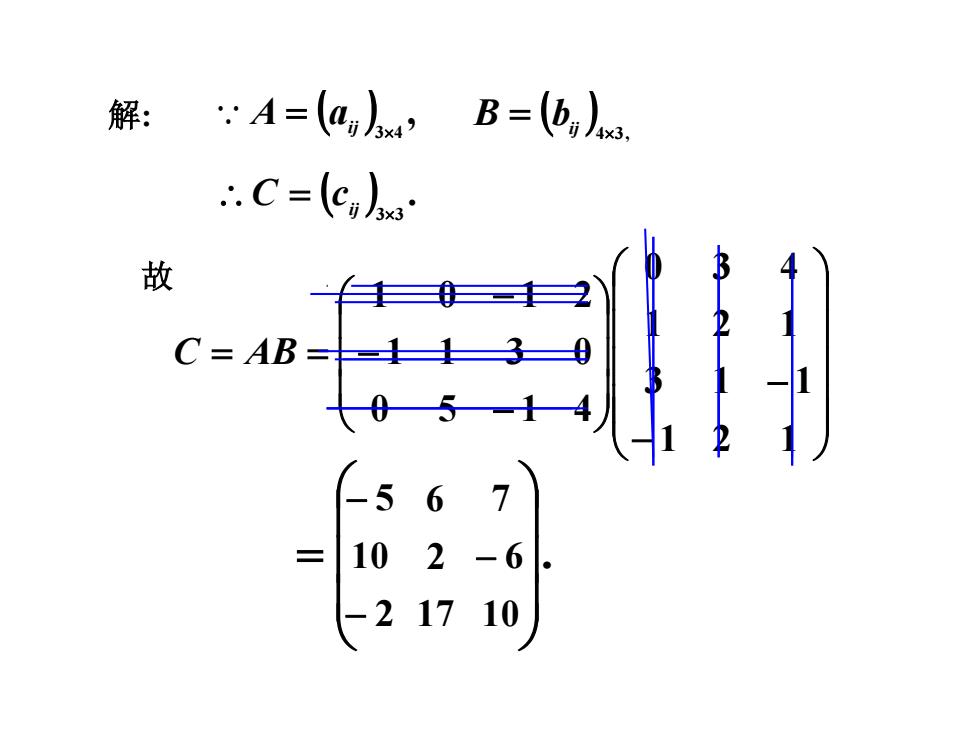
解： A=(a,人，B=(b,) .C=(ci) 故 C=AB -5 6 102-6 -21710

故               − −           − − − = = 1 2 1 3 1 1 1 2 1 0 3 4 0 5 1 4 1 1 3 0 1 0 1 2 C AB .           = 解: ( ) , 34 = ij  A a ( ) 43, B = bij ( ) . 33  = ij C c − 5 6 7 10 2 − 6 − 2 17 10

注意：只有当第一个矩阵的列数等于第二个矩阵的行数时， 两个矩阵才能相乘， 23 例如： 不存在 =1x3+2x2+3x=o

注意:只有当第一个矩阵的列数等于第二个矩阵的行数时， 两个矩阵才能相乘.                 6 0 1 1 6 8 5 8 9 3 2 1 1 2 3 例如: ( )           1 2 3 1 2 3 = (1 3 + 2 2 + 31) = (10). 不存在