海南大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵

例3：计算下列矩阵的乘积 2 () 2 1 2 3) 2 2×1 2×2 解： 2）= 2×12×2 3 3×1

例3: 计算下列矩阵的乘积. ( ) (1 2) 3 2 2 1           解: (1 2) 3 2 2                     = 21 22 21 2 2 31 3 2 . 3 6 2 4 2 4           =

(2)(6b,b 2 23 31 An b =(41b1+421b2+431h34b+a2zb2+0b413b+23b2+03b,) =a1b2+a2zb3+43b+2412bb2+2a13b,b3+223b2b3

12 1 22 2 32 3 a b + a b + a b   321 bbb 2 2 2 . 12 1 2 13 1 3 23 2 3 2 33 3 2 22 2 2 11 1 = a b + a b + a b + a b b + a b b + a b b 11 1 21 2 31 3 = ( a b + a b + a b 13 1 23 2 33 3 a b + a b + a b ） ( ) ( )    321 31 32 33 21 22 23 11 12 13 1 2 3 2 bbb a a a a a a a a a b b b

例4：计算下列矩阵的乘积. 2 14 71 214 0 = 5 -8 02 13 7 10 13 7) 3×4 2 1 21 4 5 -8 5 -8 02 10 13 7 3×4 4×4

例4： 计算下列矩阵的乘积. 3 3 3 4 10 1 3 7 5 8 0 2 1 2 1 4 1 1 1             −           4 4 3 4 1 1 1 1 10 1 3 7 5 8 0 2 1 2 1 4                           − 3 4 10 1 3 7 5 8 0 2 1 2 1 4            = − 3 4 10 1 3 7 5 8 0 2 1 2 1 4            = −

W n 20y 九. 入4g Wzy p . 01s 1021 Aaz . : : . Ay . . 20u 2 Aa . nl n2 nXI

n n ns n s s s n n n a a a a a a a a a                                       1 2 21 22 2 11 12 1 2 1    n n nn n n n n n n n a a a a a a a a a                                          2 1 1 2 21 22 2 11 12 1 n n n n n ns n s s s a a a a a a a a a                =                 1 2 2 21 2 22 2 2 1 11 1 12 1 1 n n n nn n n n n n n a a a a a a a a a                =                 1 1 2 2 1 21 2 22 2 1 11 2 12 1

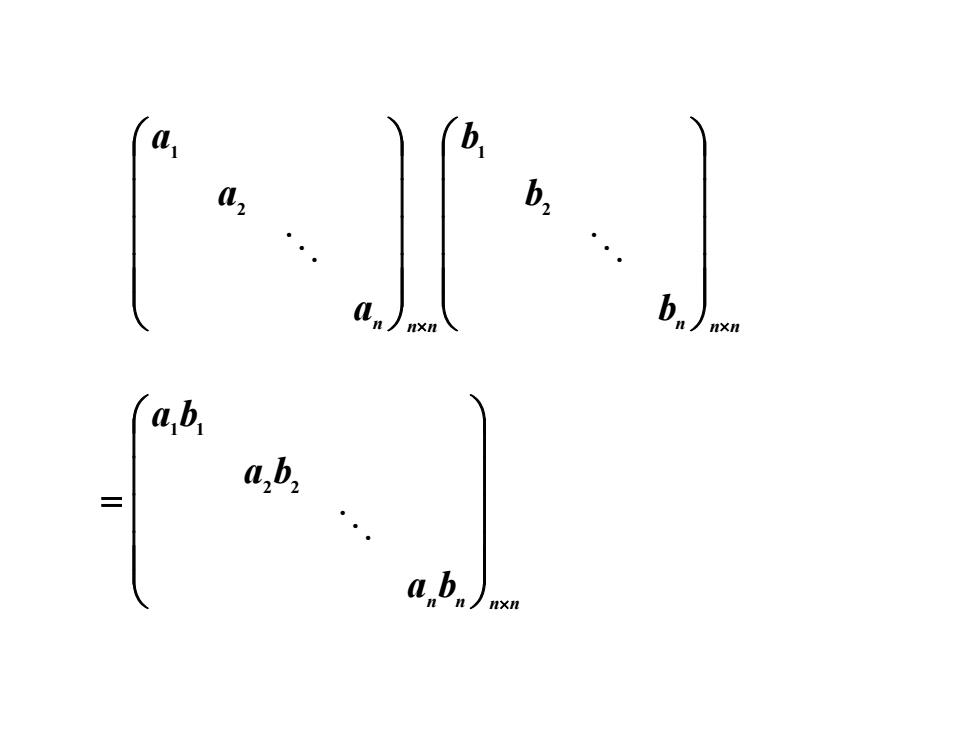
b b.) Xn ab ab, ab.) nXn

n n n n n n b b b a a a                                 2 1 2 1 n n n n a b a b a b                =  2 2 1 1