
1.矩阵相等 二.矩阵的运算 2.矩阵加减法 3.数乘矩阵 4.矩阵的乘法 1.矩阵相等. 5.矩阵的转置 6.方阵的行列式 同型矩阵:两个矩阵的行数相等、列数也相等 矩阵相等:设矩阵Amxm与Bxn是同型矩阵, 且对应元素相等,即步=,j=12m) 称矩阵A与B相等,记作A=B. -1 -1 2
二. 矩阵的运算 1.矩阵相等 2.矩阵加减法 3.数乘矩阵 4.矩阵的乘法 5.矩阵的转置 6.方阵的行列式 1. 矩阵相等. 矩阵相等: − = − − 0 2 4 3 1 0 4 1 8 z y 例: x 同型矩阵:两个矩阵的行数相等、列数也相等 . ( , 1,2,., ) A B A B i j n ij b ij a m n B m n A = = = 称矩阵 与 相等,记作 且对应元素相等,即 设矩阵 与 是同型矩阵

2.矩阵的加减法 加法: 设有两个m×n矩阵A=(a,)B=(b)那末矩阵 A与B的和记作A+B,规定为 a.+b1 a2+b2 . ain+bin 021+b21L2+b2 . azn+ban A+B=
+ + + + + + + + + + = m m m m mn mn n n n n a b a b a b a b a b a b a b a b a b A B 1 1 2 2 2 1 2 1 2 2 2 2 2 2 1 1 1 1 1 2 1 2 1 1 2. 矩阵的加减法 设有两个 矩阵 那末矩阵 与 的和记作 ,规定为 m n ( ), ( ), A = aij B = bij A B A+ B 加法:

注意:只有当两个矩阵是同型矩阵时,才能进行加法运算 例如: 12 3 -5 8 9 -9 0 6 5 4 3 6 8 3 2 1 12+1 3+8 -5+9 13 11 1+6-9+5 0+4 7 -4 4 3+36+2 8+1 6 8
注意:只有当两个矩阵是同型矩阵时,才能进行加法运算. 例如: + − − 3 2 1 6 5 4 1 8 9 3 6 8 1 9 0 12 3 5 + + + + − + + + + − + = 3 3 6 2 8 1 1 6 9 5 0 4 12 1 3 8 5 9 . 6 8 9 7 4 4 13 11 4 = −

负矩阵: 一L12 一021 一L22 一L2n -A= =(a) 一m 称为矩阵A 的负矩阵。 减法: A-B=A+(-B) 矩阵加法满足的运算规律: 交换律:A+B=B+A. 2)结合律:(A+B)+C=A+(B+C), (3)A+0=A,其中A与O是同型矩阵. (4A+(-A)=0
减法: 负矩阵: A− B = A+ (−B) − − − − − − − − − − = m m mn n n a a a a a a a a a A 1 1 21 22 2 11 12 1 ( ) = − aij 的 。 称为矩阵 负矩阵 A 矩阵加法满足的运算规律: (1) 交换律:A + B = B + A. (2) 结合律: (A + B) + C = A + (B + C). (4) A + (− A) = O. (3) A + 0 = A,其中A与O是同型矩阵
3.数与矩阵相乘 数乘:数几与矩阵A的乘积记作24A或A几,规定为 2011 212 21m 2A=A九= 2L21 2L2 注意:矩阵数乘与行列式数乘的区别. 13 2 2 05 10 5 5
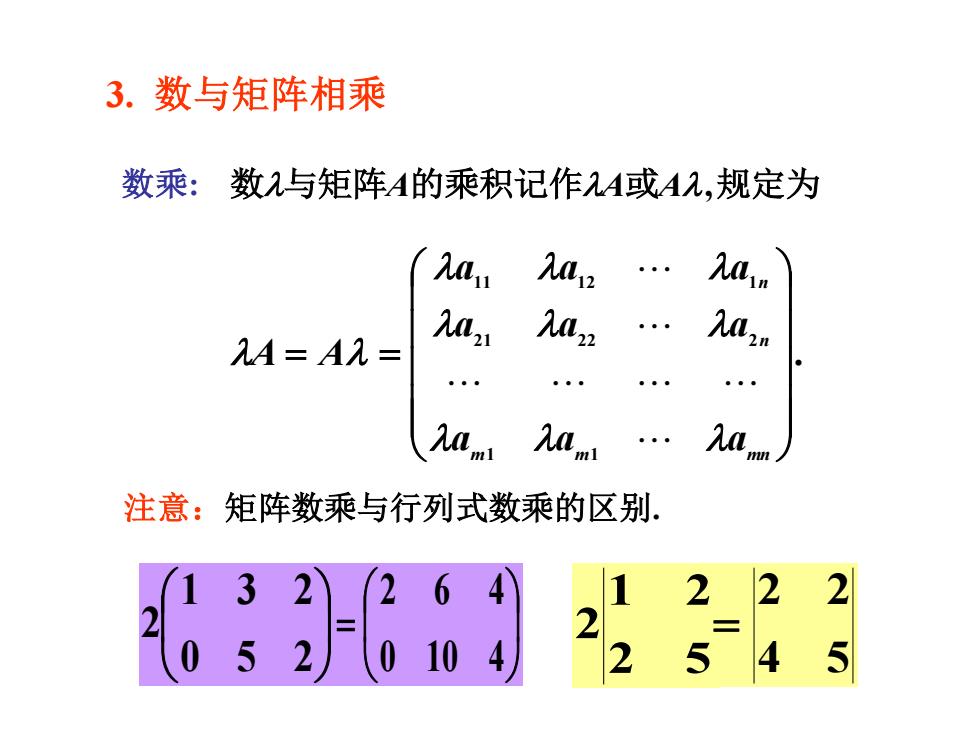
3. 数与矩阵相乘 数乘: . 1 1 21 22 2 11 12 1 = = m m mn n n a a a a a a a a a A A 数与矩阵A的乘积记作A或A,规定为 注意:矩阵数乘与行列式数乘的区别. 0 5 2 1 3 2 2 = 0 10 4 2 6 4 2 5 1 2 2 4 5 2 2 =