
导航 标准方程 点-0o0,b>0, 2个 x 2-l(a>0,b>0) 范围 ≤-M或≥y∈R -a或y2a,x∈R 性对称性 对称轴:,对称中心: 质 顶点坐标: 顶点坐标: 项点 A1,A2 A1,A2
导航 标准方程 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛𝟐 =1(a>0,b>0) 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛𝟐 =1(a>0,b>0) 性 质 范围 x≤-a 或 x≥a,y∈R y≤-a 或 y≥a,x∈R 对称性 对称轴:坐标轴,对称中心:原点 顶点 顶点坐标: A1 (-a,0) ,A2 (a,0) 顶点坐标: A1 (0,-a) ,A2 (0,a)

导航 标准方程 621(>0,b>0) 线段A1A2叫做双曲线的实轴,它的长A1A2= 实虚轴 性 线段B1B2叫做双曲线的虚轴,它的长B1B2= 渐近线 V= y= C 离心率 e=a,e∈ ,b,c的关系 c2=
导航 标准方程 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛𝟐 =1(a>0,b>0) 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛𝟐 =1(a>0,b>0) 性 质 实虚轴 线段 A1A2叫做双曲线的实轴,它的长|A1A2|= 2a , 线段 B1B2叫做双曲线的虚轴,它的长|B1B2|= 2b 渐近线 y= ± 𝒃 𝒂 x y= ± 𝒂 𝒃 x 离心率 e= 𝒄 𝒂 ,e∈(1,+∞) a,b,c 的关系 c 2 =a 2 +b2

导航、 16.抛物线的定义中应注意哪几点? 提示:()动点在平面内. (2)动点到定点F的距离与到定直线的距离相等. 3)定点不在定直线上
导航 16.抛物线的定义中应注意哪几点? 提示:(1)动点在平面内. (2)动点到定点F的距离与到定直线l的距离相等. (3)定点不在定直线上
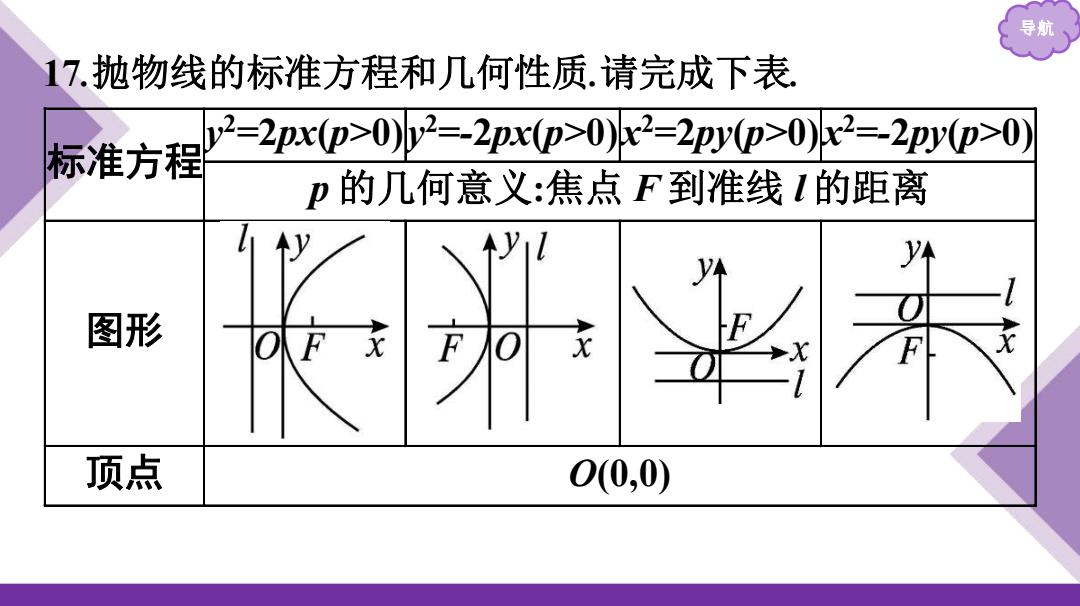
导航 17.抛物线的标准方程和几何性质.请完成下表 标准方程 y2=2pxp>0)2=-2px(p>0)lx2=2py0p>0)x2=-2pyp>0) p的几何意义:焦点F到准线1的距离 y 图形 F衣 一太 顶点 0(0,0)
导航 17.抛物线的标准方程和几何性质.请完成下表. 标准方程y 2 =2px(p>0)y 2 =-2px(p>0)x 2 =2py(p>0)x 2 =-2py(p>0) p 的几何意义:焦点 F 到准线 l 的距离 图形 顶点 O(0,0)

导航 y2=2pxp>00y2=-2px(p>0)x2=2pyp>0)x2=-2pyp>0) 标准方程 p的几何意义:焦点F到准线1的距离 对称轴 x轴 y轴 焦点 (2o) (0,) 离心率 e= 准线方程 x= x= y= y= 范围 x20y∈R s0y∈R Jy20,x∈R JSO,x∈R 开口方向 向右 向左 向上 向下
导航 标准方程y 2 =2px(p>0)y 2 =-2px(p>0)x 2 =2py(p>0)x 2 =-2py(p>0) p 的几何意义:焦点 F 到准线 l 的距离 对称轴 x 轴 y 轴 焦点 𝐩 𝟐 ,𝟎 - 𝐩 𝟐 ,𝟎 𝟎, 𝐩 𝟐 𝟎,- 𝐩 𝟐 离心率 e= 1 准线方程 x= - 𝐩 𝟐 x= 𝐩 𝟐 y= - 𝐩 𝟐 y= 𝐩 𝟐 范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R 开口方向 向右 向左 向上 向下