
导 3.做一做:y=2six的图象上各点的纵坐标不变,横坐标变为原 来的 ,得到y=2sin3x的图象,再将所得图象向左平 移个单位,得到函数 的图象 答案号-2sin(3x+》)
导航 3.做一做:y=2sin x的图象上各点的纵坐标不变,横坐标变为原 来的 ,得到y=2sin 3x的图象,再将所得图象向左平 移 个单位,得到函数 的图象. 𝛑 𝟔 答案: 𝟏 𝟑 y=2sin 𝟑𝒙 + 𝛑 𝟐

【思考辦辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√,错 误的画“X”. (1)函数y=Asin(ox+p)x∈R的最大值为A.( (2)函数y=3sin(2x-)的初相为5.() 仔)由函数-sin(x+罗)的图象得到=sinx的图象,必须向左 平移.() (4)把函数y=sinx的图象上点的横坐标变为原来的3倍就得到 函数y=sin3x的图象.()
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)函数y=Asin(ωx+φ),x∈R的最大值为A.( × ) (2)函数y=3sin(2x-5)的初相为5.( × ) (3)由函数 的图象得到y=sin x的图象,必须向左 平移.( × ) (4)把函数y=sin x的图象上点的横坐标变为原来的3倍就得到 函数y=sin 3x的图象.( × ) y=sin 𝒙 + 𝛑 𝟑

导航 课堂·重难突破 探究一用五点法作y=Asin(ox+p)的图象 【例1】 已知函数-2sin(2x-),用五点法画出其简图.。 分别令2x一3 。为 分析:五点法 →列表→描点连线. 3π 0, 2,,2,2π
导航 课堂·重难突破 探究一 用五点法作y=Asin(ωx+φ)的图象 【例 1】 已知函数 y=2sin 𝟐𝒙- 𝛑 𝟑 ,用五点法画出其简图. 分析:五点法 列表→描点→连线
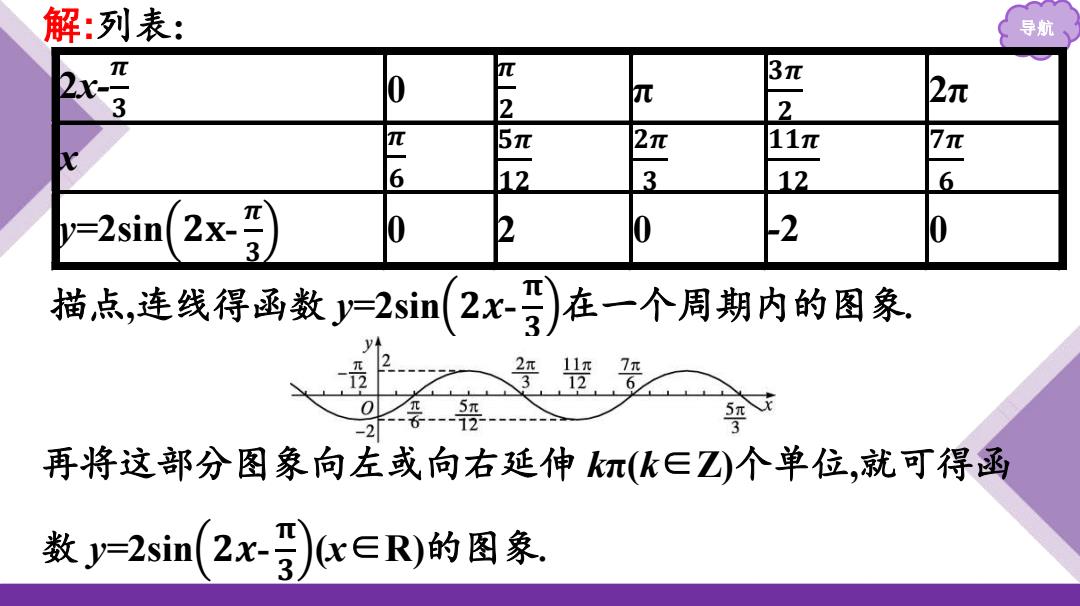
解:列表: 导航 元2 3π 2x3 0 元 2 2元 π 5π 2π 11π 6 3 12 6 y=2sin 2x-7 0 2 0 2 0 描点,连线得函数=2sin(2x)在一个周期内的图象. 5π 12 再将这部分图象向左或向右延伸π(化∈Z个单位,就可得函 数y=2sim(2x)cx∈R)的图象
解 :列表: 导航 2 x-𝝅𝟑 0 𝝅𝟐 π 𝟑 𝝅𝟐 2 π x 𝝅𝟔 𝟓𝝅𝟏𝟐 𝟐𝝅𝟑 𝟏𝟏𝝅 𝟏𝟐 𝟕𝝅𝟔 y=2sin 𝟐 𝐱- 𝝅𝟑 0 2 0 -2 0 描点,连线得函数 y=2sin 𝟐 𝒙- 𝛑𝟑 在一个周期内的图 象. 再将这部分图 象向左或向右延伸 kπ(k ∈ Z)个单位,就可得函 数 y=2sin 𝟐 𝒙- 𝛑𝟑 (x ∈ R)的图 象