《线性代数》课程PPT教学课件（B）第三章 矩阵运算_3-1矩阵的运算

1 l12 s 21 02 02s Ls .b 41b1+.+41,b,1. 41b1n+.+41sbm a2ib1+.+a2,b,1.ab++.+a2,bm amb+.+anmb,1.Ambin+.+anbn」

11 12 1 11 12 1 21 22 2 21 22 2 1 2 1 2 11 11 1 1 11 1 1 21 11 2 1 21 1 2 1 11 1 1 1 s n s n m m ms s s sn s s n s sn s s n s sn m ms s m n ms sn a a a b b b a a a b b b a a a b b b a b a b a b a b a b a b a b a b a b a b a b a b +               + + + +   + + + + = + + + +  

关于定义说明： (①)只有当左边矩阵A的列数等于右边矩阵B的行数时， A,B才可乘积，AB才有意义 例如 不存在。 (2)AB的行数等于矩阵A的行数，AB的列数等于矩阵 B的列数 (3)AB的第行第列的元素c,等于矩阵A的第行元素 与矩阵B的第列元素对应乘积之和

1 2 3 1 6 8 3 2 1 6 0 1 589              例如 不存在. 关于定义说明: , , . (1) , 才可乘积 才有意义 只有当左边矩阵 的列数等于右边矩阵 的行数时 A B AB A B . (2) , 的列数 的行数等于矩阵 的行数 的列数等于矩阵 B AB A AB . (3) 与矩阵 的第 列元素对应乘积之和 的第 行第 列的元素 等于矩阵 的第 行元素 B j AB i j c A i i j

借助矩阵的乘法，线性方程组可以表示为 01火1+412火2+.41mXn=b1 021X1+422X2+.2mXn=b2 0mlX1+m2X2+.mnXn=bm 中令 12 b 。 A= ,X= ，B= n 则方程组可以表示为矩阵形式AX=B

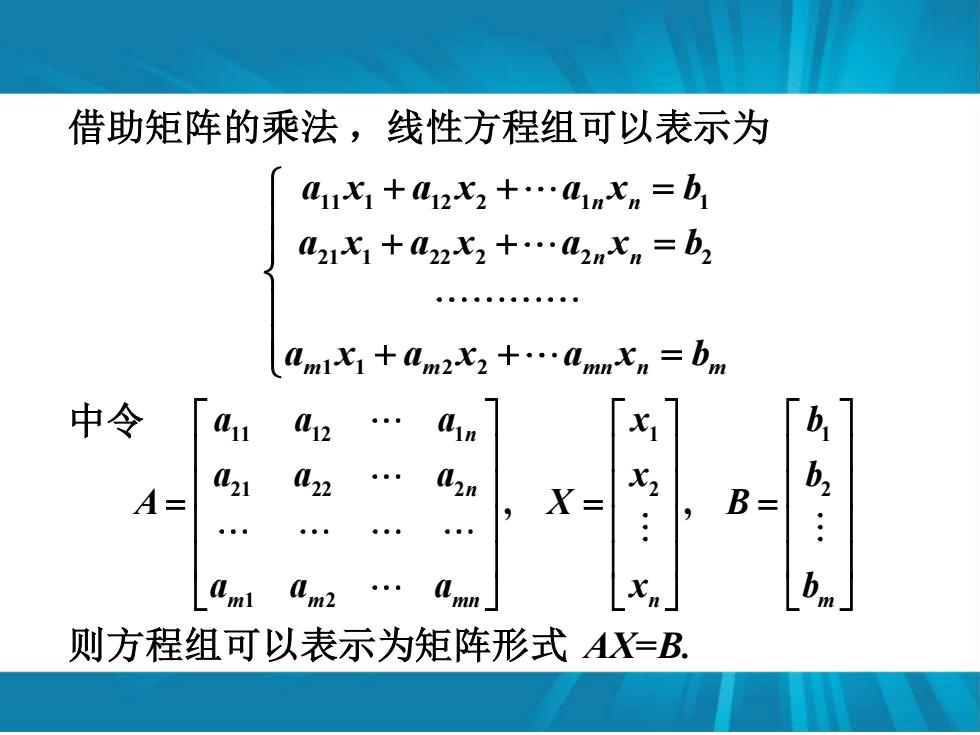
借助矩阵的乘法 ，线性方程组可以表示为 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + =   + + =     + + = 中令 11 12 1 1 1 21 22 2 2 2 1 2 , , n n m m mn n m a a a x b a a a x b A X B a a a x b                   = = =                   则方程组可以表示为矩阵形式 AX=B

1 2 1 0 2 -1 2 1 例3设A= 01 -1 3 B= ,求AB. 0 3 -120 1 .4 解： 1x1+0x2+2×0-1×11×2+0x1+2x3-1×4 AB= 0x1+1×2-1×0+3×10×2+1x1-1×3+3×4 -1×1+2×2+0x0+1×1-1×2+2×1+0x3+1×4 0 4 = 5 10 4 4

1 2 1 0 2 1 2 1 3 0 1 1 3 , , . 0 3 1 2 0 1 1 4 A B AB     −     = − =           −     例 设 求 解: 1 1 0 2 2 0 1 1 1 2 0 1 2 3 1 4 0 1 1 2 1 0 3 1 0 2 1 1 1 3 3 4 1 1 2 2 0 0 1 1 1 2 2 1 0 3 1 4 AB    +  +  −   +  +  −    =  +  −  +   +  −  +      −  +  +  +  −  +  +  +    0 4 5 10 4 4     =      