《线性代数》课程PPT教学课件（B）第三章 矩阵运算_3-1矩阵的运算

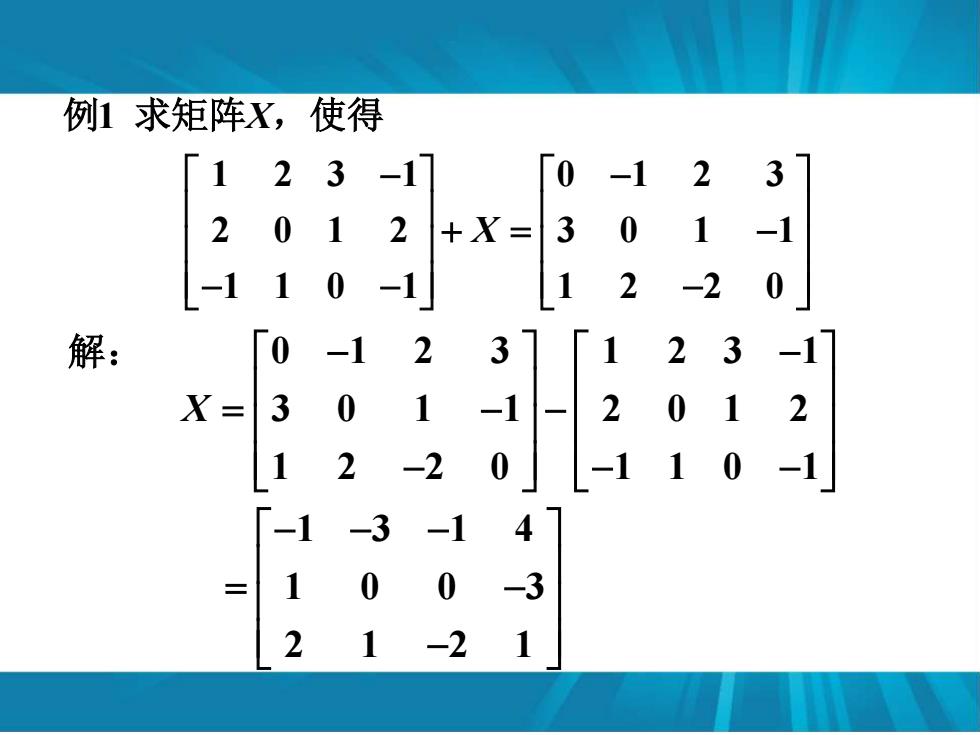
例1求矩阵X,使得 123 -17 0 -1 23 2 0 1 2+X= 3 0 1-1 -11 0 -1 1 2 -2 0 解： To -1 2 3 1 2 ● -1 X= 3 0 -1 一 2 0 2 1 2 -2 0 -11 0 -1 -1 -3 -1 4 1 0 0 -3 2 1 -2

1 1 2 3 1 0 1 2 3 2 0 1 2 3 0 1 1 1 1 0 1 1 2 2 0 X X     − −     + = −             − − − 例 求矩阵 ，使得 解： 0 1 2 3 1 2 3 1 3 0 1 1 2 0 1 2 1 2 2 0 1 1 0 1 X     − −     = − −             − − − 1 3 1 4 1 0 0 3 2 1 2 1   − − −   = −       −

三、数与矩阵的乘法 定义3.1.2设矩阵A=(ag)xn,是一个数，矩阵 (几a,)mx,称为数入与矩阵A的乘积，记作九A或A几， 即 2A=A久=(2L时)）mxn 注：数乘矩阵与数乘行列式是显然是不同的. ()数称行列式是数乘到行列式的其中一行或列上， (2)数乘矩阵是数乘到矩阵的每一行的每一个元素上

三、数与矩阵的乘法 ( ) , , ( ) ( ) 3.1.2 ij m n ij m n ij m n A a a A A A A a A            = = = 数 设矩阵 是一个数 矩阵 称为 记作 或 ， 即 与矩阵 ， 定 的乘积 义 注：数乘矩阵与数乘行列式是显然是不同的. (1)数称行列式是数乘到行列式的其中一行或列上. (2)数乘矩阵是数乘到矩阵的每一行的每一个元素上

数乘的性质： 设A,B是m×n矩阵，几，u是数， 1.兄（山A)=(兄）A 2.(+☑)A=兄A+uA 3.几(A+B)=入A+入B 4.1A=A 5.0A=0 6.(-1)A=-A

数乘的性质： 2. ( )     + = + A A A 设A B m n ， 是  矩阵， , 是数， 3. ( )    A B A B + = + 1. ( ) ( )    A A = 4. 1A A = 5. 0A O= 6. ( 1) − = − A A

咖w:8-[1g c-[位6可4- 解： 1 [4-1-10+1+2-2-0+1 2A-B+ C= 3 2+2+44-3-2-4-1+3 23-1 8-1-2

2 0 1 1 1 0 2 , , 1 2 2 2 3 1 3 6 3 1 2 . 12 6 9 3 A B C A B C     − − = =         − −   − = − +     − 例 设 ,求 1 4 1 1 0 1 2 2 0 1 2 3 2 2 4 4 3 2 4 1 3 A B C   − − + + − − + − + =     + + − − − − + 2 3 1 8 1 2   − =     − − 解：

四、矩阵的乘法 1.定义 定义3.1.3设A=(a)是一个m×s矩阵，B=(b) 是一个s×nm矩阵，作m×n矩阵C=(c),其中 c与=a+a,b,++ab,=∑abg 矩阵C称为矩阵A与矩阵B的乘积， 记作C=AB,即

1 1 2 2 1 ( ) , ( ) , ( ) 3.1.3 , ij ij ij s ij i j i j is sj ik kj k A a m s B b s n m n C c c a b a b a b a b C A B C AB = =  =   = = + + + = =  设 是一个 矩阵 是一个 矩阵 作 矩阵 ，其中 ， 矩阵 称为矩阵 与矩阵 的 ， 记作 乘积 定义 即 1.定义 四、矩阵的乘法