海南大学：《线性代数》课程教学资源（PPT课件）第三章 矩阵的初等变换与线性方程组

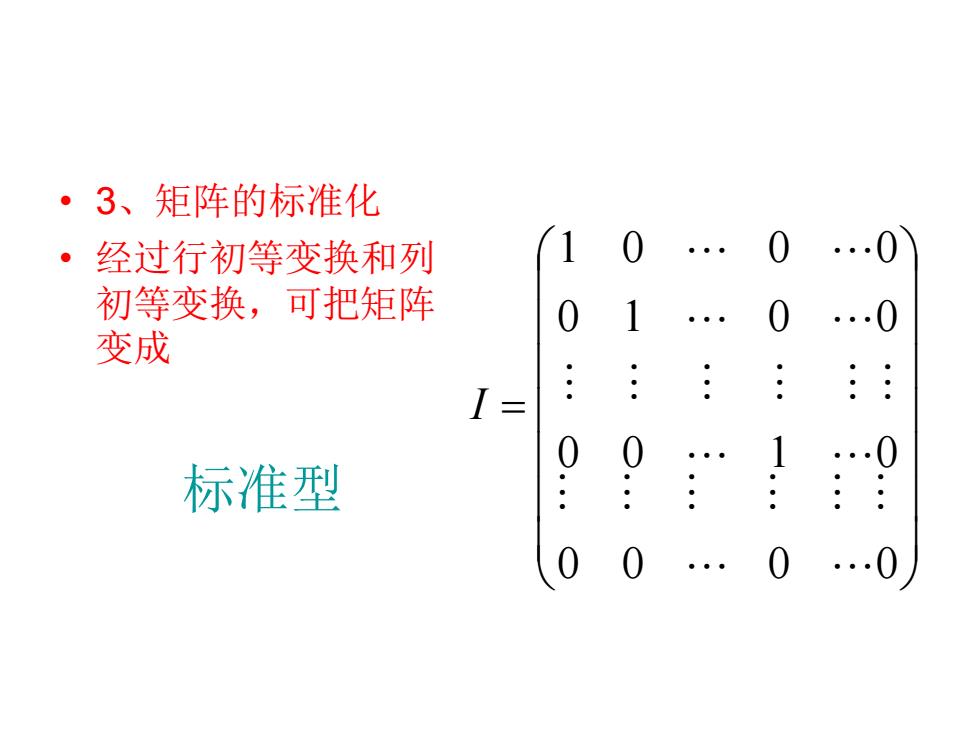
·3、矩阵的标准化 ·经过行初等变换和列 初等变换，可把矩阵 0 变成 .: I= 0 标准型 00

• 3、矩阵的标准化 • 经过行初等变换和列 初等变换，可把矩阵 变成                   = 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0                     I 标准型

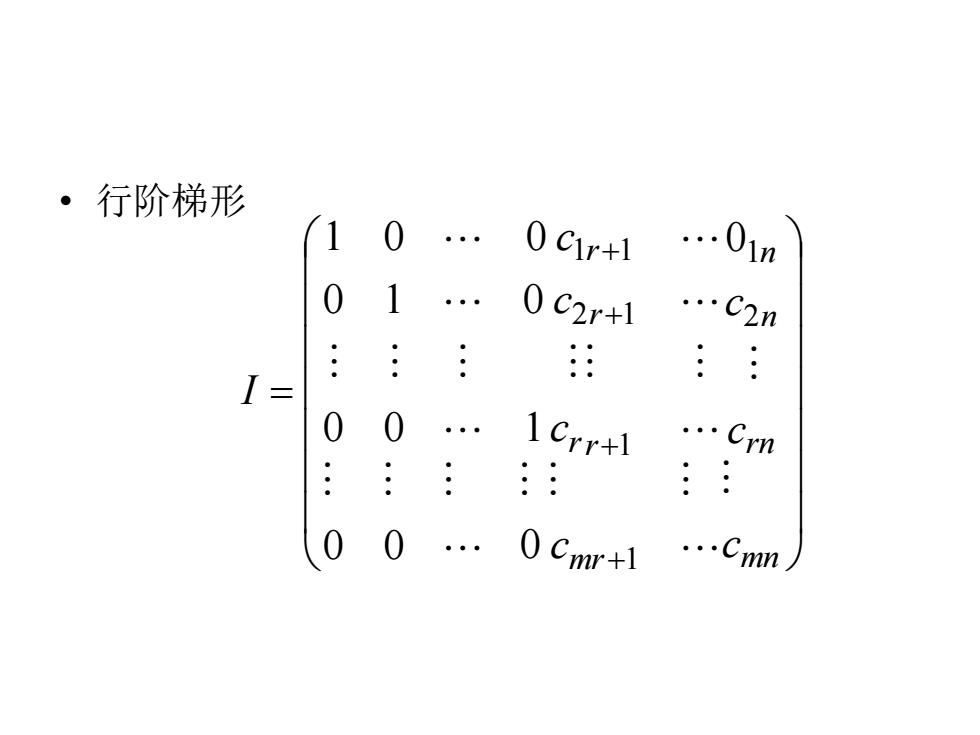
·行阶梯形 1 0. 0C1r 1.01n 0 1 0C2r+1 .C2n .: : I= 0 0 1Crr+l .Crn : : 00 .0Cr+1 .Cmn

• 行阶梯形                   = + + + + mn rn n n mr rr r r c c c c c c c I                      2 1 1 1 2 1 1 1 0 0 0 0 0 0 1 0 1 0 1 0 0

·列最简形式 0 0 1=0 0 0 Cr+11 Cr+12 Cr+lr .Cr+1n Cml Cm2 . Cmr .Cm

• 列最简形式                     = + + + + mn r n m m mr r r r r c c c c c c c c I                       1 1 2 11 12 1 0 0 0 0 0 1 0 1 0 1 0 0

第二节.初等矩阵 矩阵初等变换是矩阵的一种基本运算，应用广泛. 定义3：由单位矩阵E经过一次初等变换得到的方 阵称为初等矩阵. 三种初等变换对应着三种初等方阵 「1.对调两行或两列； 2.以数k≠0乘某行或某列； 3.以数k乘某行（列）加到另一行（列)上去

定义3：由单位矩阵 经过一次初等变换得到的方 阵称为初等矩阵. E 三种初等变换对应着三种初等方阵. 矩阵初等变换是矩阵的一种基本运算，应用广泛.       以数 乘某行（列）加到另一行（列）上去． 以数 乘某行或某列； 对调两行或两列； k k 3. 2. 0 1. 第二节. 初等矩阵

(1)对调两行或两列，得初等对换矩阵。 对调E中第i,j两行，即()，得初等方阵 ←第i行 E(i,j)= ←第j行

对调 E 中第 i, j 两行，即(ri  rj )，得初等方阵                                   = 1 1 1 0 1 1 0 1 1 1 ( , )        E i j  第 i 行  第 j 行 (1) 对调两行或两列，得初等对换矩阵