海南大学：《线性代数》课程教学资源（PPT课件）第三章 矩阵的初等变换与线性方程组

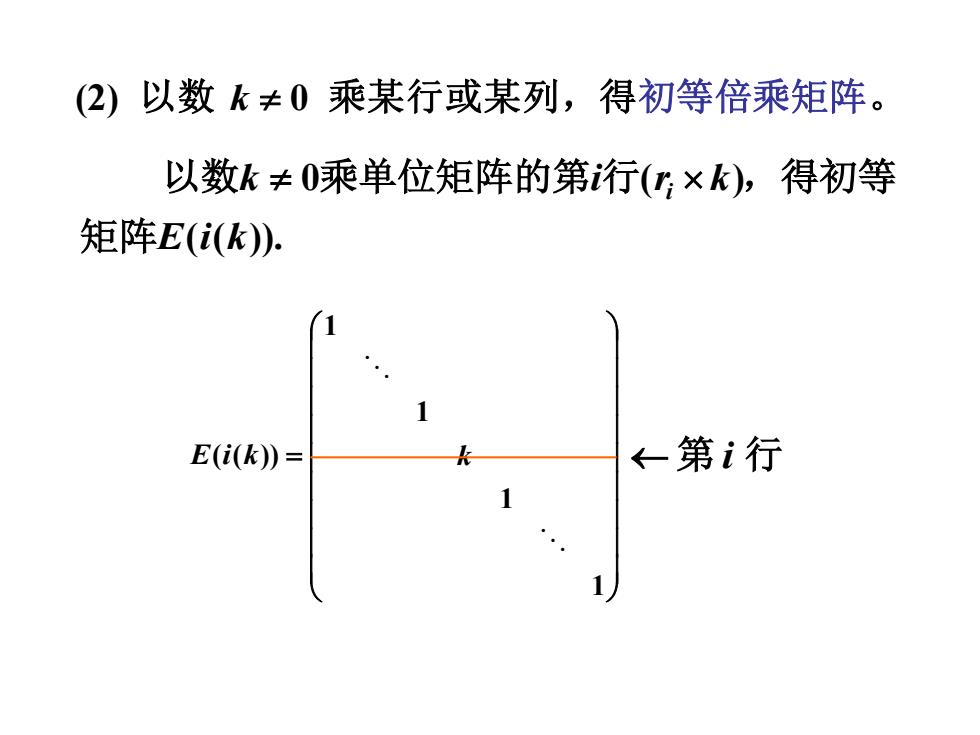
(2)以数k≠0乘某行或某列，得初等倍乘矩阵。 以数k≠0乘单位矩阵的第行(y:×k),得初等 矩阵E(i(k) E(i(k= ←第i行

( ( )). 0 ( ) E i k k i ri k 矩阵 以数  乘单位矩阵的第 行  ，得初等                       = 1 1 1 1 ( ( ))   E i k k  第 i 行 (2) 以数 k  0 乘某行或某列，得初等倍乘矩阵

(3)以数k≠0乘某行（列）加到另一行（列）上， 得初等倍加矩阵。 以k乘E的第j行加到第i行上(+kr) [或以k乘E的第i列加到第j列上(c,+kc), ←第行 E(ij(k= ←第行

或以 乘 的第 列加到第 列上 ， 以 乘 的第 行加到第 行上 [ ( ) ( ) j i i j k E i j c kc k E j i r kr + +                       = 1 1 1 1 ( ( ))     k E ij k  第i行  第j行 (3) 以数 k  0 乘某行（列）加到另一行（列）上， 得初等倍加矩阵

初等矩阵是可逆的，逆矩阵仍为初等矩阵。 变换→”的逆变换是其本身， 则E(i,)1=E(i,j); 变换×k的逆变换为×？ 则E(k)》=E(片 变换×kr,的逆变换为×(-k)r 则E((k)1=E((-k)

( , ) ( , ) 则 1 ； 变换 的逆变换是其本身， E i j E i j r r i j =  − )); 1 ( ( )) ( ( 1 1 k E i k E i k r k r i i =   则 − 变换 的逆变换为 ， ( ( )) ( ( )) . ( ) 1 E ij k E ij k r kr r k r i j i j = −   − 则 − 变换 的逆变换为 ， 初等矩阵是可逆的，逆矩阵仍为初等矩阵

初等变换 初等矩阵 初等逆变换 初等逆矩阵 例1：计算 (100a1 12 n 11 %12 n (1) 0k0 22 kaz kaz . 00 1 31 L32 L31 2

初等变换 初等矩阵 初等逆变换 初等逆矩阵 例1：计算 11 12 1 21 22 2 31 32 3 1 0 0 (1) 0 0 0 0 1 n n n a a a k a a a a a a                11 12 1 21 22 2 31 32 3 n n n a a a ka ka ka a a a     =      

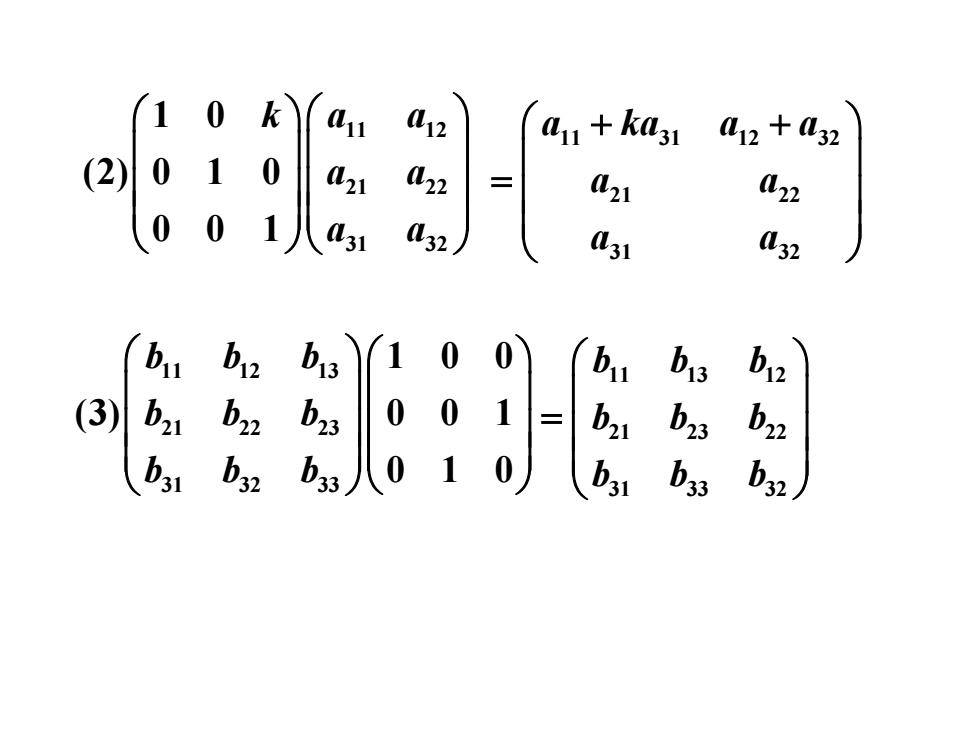
10k 12 a11+ka31 12+32 2) 01 00 1 A22 032 431 M32 （b bi3 b2 (3) bis b2 b31 b33

11 12 21 22 31 32 1 0 (2) 0 1 0 0 0 1 k a a a a a a                11 31 12 32 21 22 31 32 a ka a a a a a a   + +   =       11 12 13 21 22 23 31 32 33 1 0 0 (3) 0 0 1 0 1 0 b b b b b b b b b                11 13 12 21 23 22 31 33 32 b b b b b b b b b     =      