
思路点拨:(1)连接GC,△ADG与△CDG全等吗?由此可得线 段AG与CG具有什么数量关系?在Rt△GEC中,线段CG,GE, EC有什么数量关系? (2)作AH⊥BD于点H,则△ABH与△AGH有何特点?BH,HG 与BG有何数量关系?
思路点拨:(1)连接GC,△ADG与△CDG全等吗?由此可得线 段AG与CG具有什么数量关系?在Rt△GEC中,线段CG,GE, EC有什么数量关系? (2)作AH⊥BD于点H,则△ABH与△AGH有何特点?BH,HG 与BG有何数量关系?
解:1)AG2=GE2+GF2.理由如下:连接GC, 由正方形的性质知AD=CD,∠ADG=∠CDG. 在△ADG和△CDG中, A G .AD=CD,∠ADG=∠CDG,GD=GD, E .△ADG≈△CDG,∴AG=CG. 由题意知∠GEC=∠GFC=∠DCB=0°, .四边形GFCE是矩形,.GF=EC B F 在Rt△GEC中,根据勾股定理, 得GC2=GE2+EC2,∴.AG2=GE2+GF2
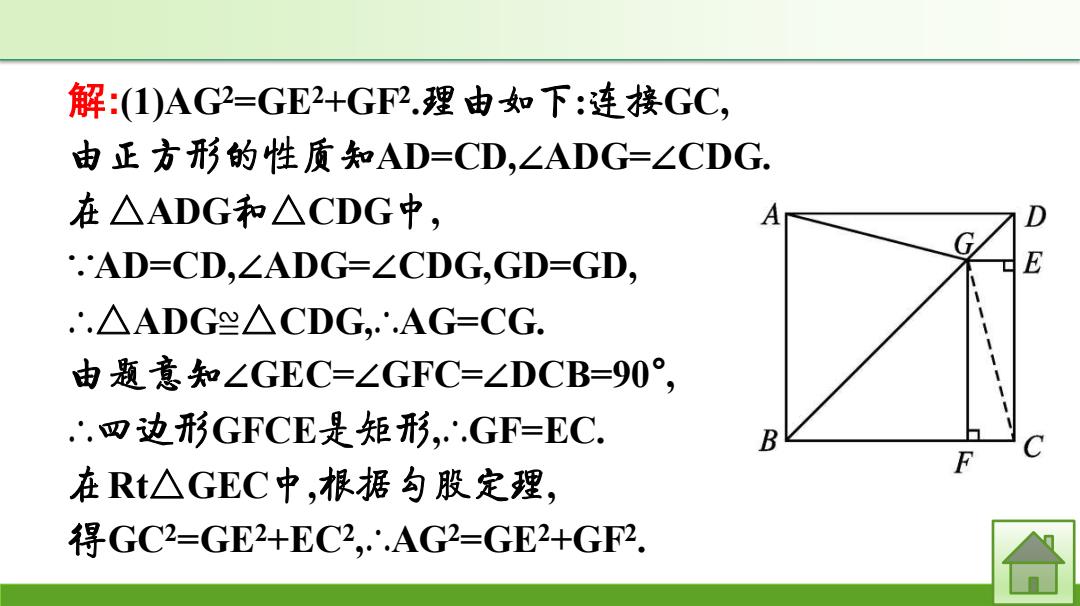
解:(1)AG2=GE2+GF2 .理由如下:连接GC, 由正方形的性质知AD=CD,∠ADG=∠CDG. 在△ADG和△CDG中, ∵AD=CD,∠ADG=∠CDG,GD=GD, ∴△ADG≌△CDG,∴AG=CG. 由题意知∠GEC=∠GFC=∠DCB=90° , ∴四边形GFCE是矩形,∴GF=EC. 在Rt△GEC中,根据勾股定理, 得GC2=GE2+EC2 ,∴AG2=GE2+GF2