
欧拉公式 定理17.8(欧拉公式)设G为n阶m条边r个面的连通平面图, 则n-H=2. 证对边数m做归纳证明. =0,G为平凡图,结论为真, 设=k(21)结论为真,m=k+1时分情况讨论如下: (1)G中无圈,则G必有一个度数为1的顶点,删除v及它关 联的边,记作G.G连通,有n-1个顶点,k条边和个面.由归 纳假设,(n-1)-k+=2,即-(k+1)+=2,得证n=k+1时结论成立. (2)否则,删除一个圈上的一条边,记作G'.G连通,有个顶 点,k条边和r-1个面.由归纳假设,-k+(-1)=2,即-(k+1)+=2, 得证k+1时结论也成立.证毕
欧拉公式 定理17.8 (欧拉公式) 设G为n阶m条边r个面的连通平面图, 则 nm+r=2. 证 对边数m做归纳证明. m=0, G为平凡图, 结论为真. 设m=k(k1)结论为真, m=k+1时分情况讨论如下: (1) G中无圈, 则G必有一个度数为1的顶点v, 删除v及它关 联的边, 记作G . G连通, 有n-1个顶点, k条边和r个面. 由归 纳假设, (n-1)-k+r=2, 即n-(k+1)+r=2, 得证m=k+1时结论成立. (2) 否则,删除一个圈上的一条边,记作G . G连通, 有n个顶 点,k条边和r-1个面. 由归纳假设, n-k+(r-1)=2, 即n-(k+1)+r=2, 得证m=k+1时结论也成立. 证毕

欧拉公式(续) 定理17.9 欧拉公式的推广 设G是有p≥2)个连通分支的平面图,则 n-m+r=p+1 证设第i个连通分支有n,个顶点,m,条边和r:个面, 对各连通分支用欧拉公式, n:-m+:=2,i=1,2,.,p 求和并注意r=r++r+p-1,即得 n-m+r=p+1
欧拉公式(续) 定理17.9 欧拉公式的推广 设G是有 p (p2) 个连通分支的平面图, 则 n m + r = p + 1 证 设第 i 个连通分支有 ni个顶点, mi条边和 ri个面. 对各连通分支用欧拉公式, ni mi + ri = 2, i = 1, 2, . , p 求和并注意 r = r1+.+rp + p1, 即得 n m + r = p + 1
与欧拉公式有关的定理 定理17.10设G为n阶连通平面图,有m条边,且每个面的次数 不小于23,1≤)n-2 证由定理(各面次数之和等于边数的2倍)及欧拉公式得 2m≥lr=l(2+m-n) 可解得所需结论. 推论K和K,3不是平面图。 证用反证法,假设它们是平面图, MM 则K:n=5,=10,-3 V K3,3:n=6,F9,=4 与定理17.8矛盾. K 3
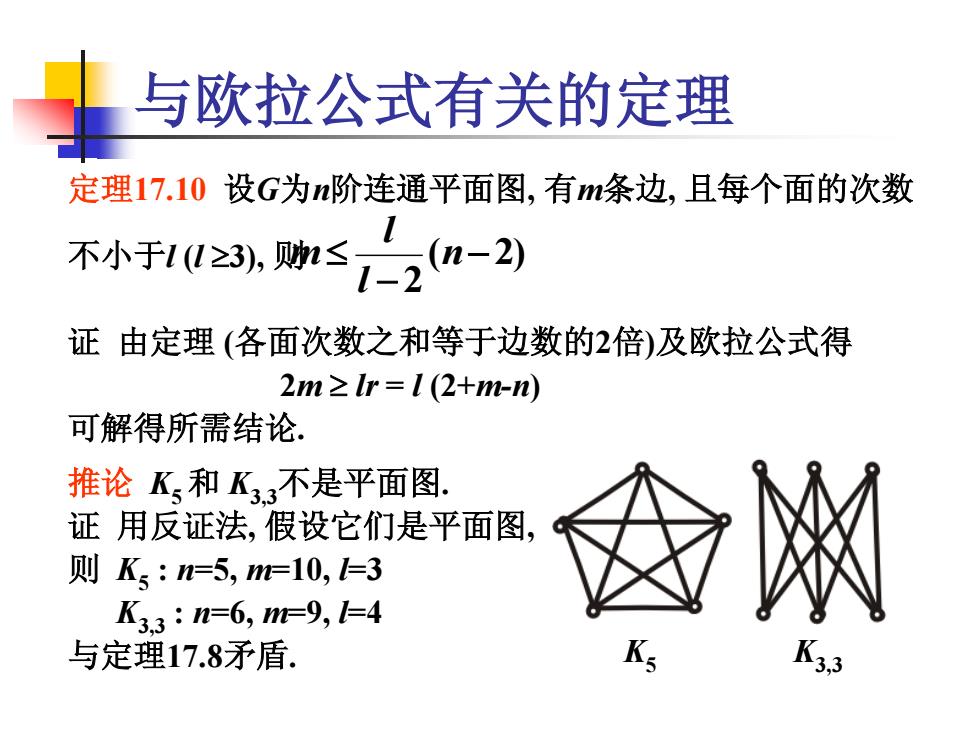
与欧拉公式有关的定理 ( 2) 2 n l l m K5 K3,3 定理17.10 设G为n阶连通平面图, 有m条边, 且每个面的次数 不小于l (l 3), 则 证 由定理 (各面次数之和等于边数的2倍)及欧拉公式得 2m lr = l (2+m-n) 可解得所需结论. 推论 K5 和 K3,3不是平面图. 证 用反证法, 假设它们是平面图, 则 K5 : n=5, m=10, l=3 K3,3 : n=6, m=9, l=4 与定理17.8矛盾