
图的运算 16 GUG:以V(G)UV(G)中的顶点组成的集合为顶点 集,以E(G)UE(G)为边集。∥简单图的并 口假设G和G是不交的无向图,定义G*G如下: 口以V(G)UV(G)为顶点集 以E(G)UE(G)U{x,x∈V(G),y∈V(G)}为边集 口举例,K2*K3=K5 简单图G的补图(complement graph),记为G 口G=(V,E)的补图定义为(V,V2E)
G∪G’:以V(G)∪V(G’)中的顶点组成的集合为顶点 集,以E(G)∪E(G’)为边集。 //简单图的并 假设G和G’是不交的无向图, 定义GG’如下: 以V(G)∪V(G’)为顶点集 以E(G)∪E(G’)∪{{x, y}| xV(G), yV(G’)}为边集 举例, K2 K3 = K5 . 简单图G的补图(complement graph),记为 G G=(V, E) 的补图定义为(V, [V]2 \E) 16 图的运算

本节提要 17 口内容1:图的定义 ▣内容2:图的应用 口内容3:图的表示 ▣内容4:图的同构
本节提要 内容1:图的定义 内容2:图的应用 内容3:图的表示 内容4:图的同构 17

图模型 18 口交通网络 口航空、公路、铁路 口信息网络 o万维网图(Web Graph) o引用图(Citation Graph) 0 社会网络 口熟人关系图 口合作图,好莱坞图 口呼叫图 口体育(循环赛的图模型)
交通网络 航空、公路、铁路 信息网络 万维网图(Web Graph) 引用图(Citation Graph) 社会网络 熟人关系图 合作图,好莱坞图 呼叫图 体育(循环赛的图模型) 18 图模型

Konigsberg-七桥问题 19 口问题的抽象: 口用顶点表示对象“地块” 口用边表示对象之间的关系“有桥相连” B B
Königsberg七桥问题 问题的抽象: 用顶点表示对象-“地块” 用边表示对象之间的关系-“有桥相连” C D A B A C B D 19
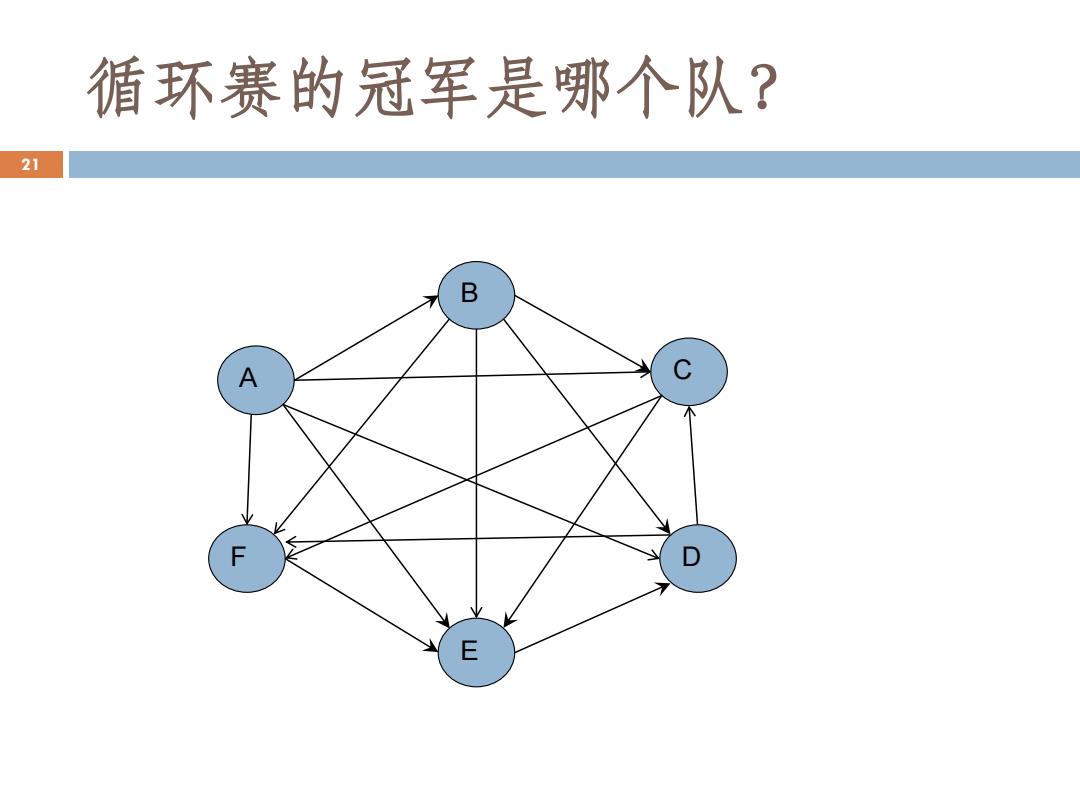
循环赛的冠军是哪个队? 21 B A C F D E
循环赛的冠军是哪个队? A B C F E D 21