
模型2 Logistic模型 dN =k(K-N)N dt 该式还有另一解释,由于空间和资源都是有限的,不可 能供养无限增长的种群个体,当种群数量过多时,由于人均 资源占有率的下降及环境恶化、疾病增多等原因,出生率将 降低而死亡率却会提高。设环境能供养的种群数量的上界为 K(近似地将K看成常数),N表示当前的种群数量,K-N恰 为环境还能供养的种群数量,该式指出,种群增长率与两者 的乘积成正比,正好符合统计规律,得到了实验结果的支持, 这就是该式也被称为统计筹算律的原因。 求解—分离变量: (+N dN kKdt 两边积分并整理得: K N= 1+Ce-kKr
模型2 Logistic模型 ( ) dN k K N N dt 该式还有另一解释,由于空间和资源都是有限的,不可 能供养无限增长的种群个体,当种群数量过多时,由于人均 资源占有率的下降及环境恶化、疾病增多等原因,出生率将 降低而死亡率却会提高。设环境能供养的种群数量的上界为 K(近似地将K看成常数),N表示当前的种群数量,K-N恰 为环境还能供养的种群数量,该式指出,种群增长率与两者 的乘积成正比,正好符合统计规律,得到了实验结果的支持, 这就是该式也被称为统计筹算律的原因。 求解——分离变量: 1 1 dN kKdt N K N 两边积分并整理得: 1 kKt K N Ce

K N= 1+Ce-kKT 令N(O)=N,求得: c- K-No No 故满足初始条件N(O)=WN的解为: N(t)= NoK N。+(K-No)e 易见: 1.5 N(0)=No ,lim N(t)=K N0=1.5 Logistic曲线 t)400 1 N()的图形请看右图 K=1 0.5 NoK N0=0.1 N()= N。+(K-N)e" 0 0 10 20 30 40 50
1 kKt K N Ce 令N(0)=N0,求得: 0 0 K N C N 故满足初始条件N(0)=N0的解为: 0 0 0 ( ) ( ) kKt N K N t N K N e 易见: N(0)=N0 ,lim ( ) t N t K N(t)的图形请看右图 rt N K N e N K N t ( ) ( ) 0 0 0
模型的参数估计 用指数增长模型或阻滞增长模型作人口预报, 必须先估计模型参数r或r,K 利用统计数据用最小二乘法作拟合 例:美国人口数据 (单位~百万) 17901800181018201830 1950 1960 1970 1980 3.9 5.37.2 9.6 12.9 150.7179.3204.0226.5 =0.2072.K=464 专家估计
模型的参数估计 用指数增长模型或阻滞增长模型作人口预报, 必须先估计模型参数 r 或 r, K • 利用统计数据用最小二乘法作拟合 例:美国人口数据(单位~百万) 1790 1800 1810 1820 1830 …… 1950 1960 1970 1980 3.9 5.3 7.2 9.6 12.9 …… 150.7 179.3 204.0 226.5 r=0.2072, K=464 • 专家估计

模型检验(1) 用模型预报1990年美国人口,与实际数据比较 x(1990=x(1980+△x=x(1980+x(19801-x(1980/xml x(1990)=250.5 实际为251.4(百万) 模型应用 人口预报 用美国1790~1990年人口数据重新估计参数 实际: W(2000)=275.0 282.4 r=0.2083,N=457.6 W(2010)=297.9 310.4 L0gSic模型在经济领域中的应用(如耐用消费品的鲁量)
模 型 检 验(1) 用模型预报1990年美国人口,与实际数据比较 (1990) (1980) (1980) (1980)[1 (1980)/ ] m x x x x rx x x x(1990) 250.5 实际为251.4 (百万) 模 型 应 用——人 口 预 报 用美国1790~1990年人口数据重新估计参数 r=0.2083, N=457.6 N(2000)=275.0 N(2010)=297.9 Logistic模型在经济领域中的应用(如耐用消费品的售量) 实际: 282.4 310.4
模型检验(2) 用Logisticz模型来描述种群增长的规律效果如何呢?1945 年克朗皮克(Crombic)做了一个人工饲养小谷虫的实验,数 学生物学家高斯(E.F.Gauss)也做了一个原生物草履虫实验, 实验结果都和Logistic曲线十分吻合。 大量实验资料表明用Logistic模型来描述种群的增长,效 果还是相当不错的。例如,高斯把5只草履虫放进一个盛有 0.5cm3营养液的小试管,他发现,开始时草履虫以每天230.9% 的速率增长,此后增长速度不断减慢,到第五天达到最大量 375个,实验数据与=2.309,=0.006157,N(0)=5的L0 gistic 曲线: 375 400 N(t)= 1+74e2309几乎完全吻合。 K375 300 200 100N0=5 C.F.Gauss 0 0
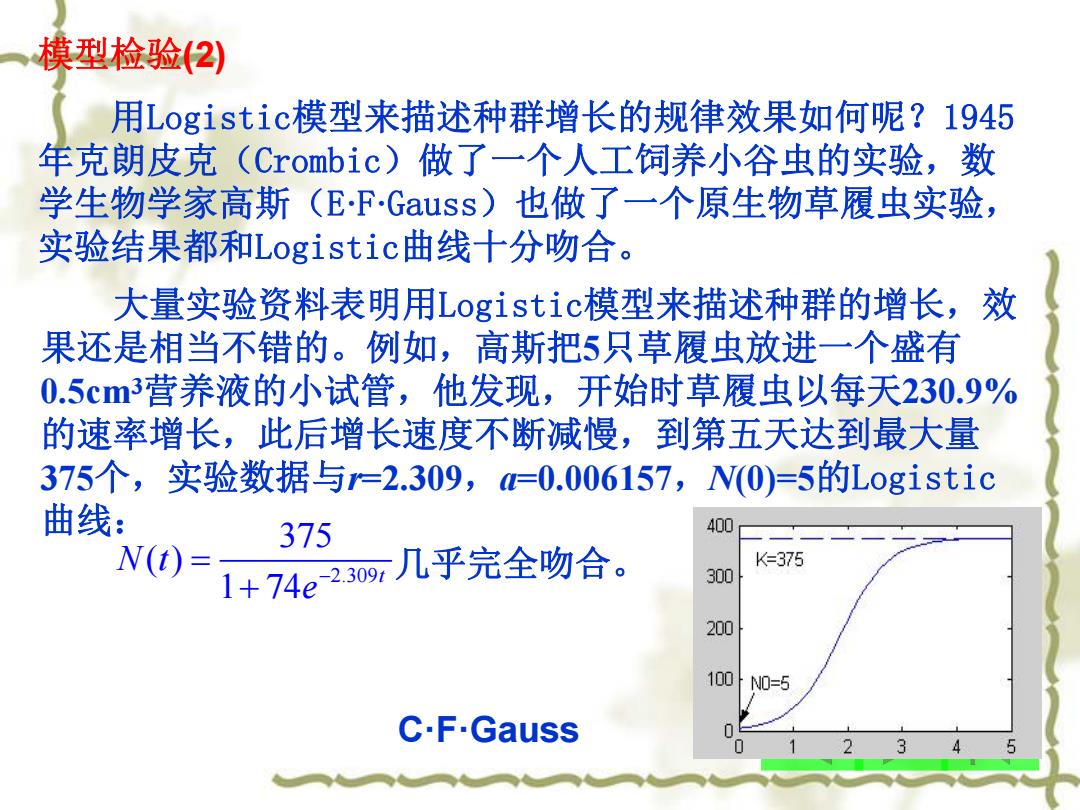
模型检验(2) 用Logistic模型来描述种群增长的规律效果如何呢?1945 年克朗皮克(Crombic)做了一个人工饲养小谷虫的实验,数 学生物学家高斯(E·F·Gauss)也做了一个原生物草履虫实验, 实验结果都和Logistic曲线十分吻合。 大量实验资料表明用Logistic模型来描述种群的增长,效 果还是相当不错的。例如,高斯把5只草履虫放进一个盛有 0.5cm3营养液的小试管,他发现,开始时草履虫以每天230.9% 的速率增长,此后增长速度不断减慢,到第五天达到最大量 375个,实验数据与r=2.309,a=0.006157,N(0)=5的Logistic 曲线: 2.3 0 9 几乎完全吻合。 375 ( ) 1 74 N t t e C·F·Gauss