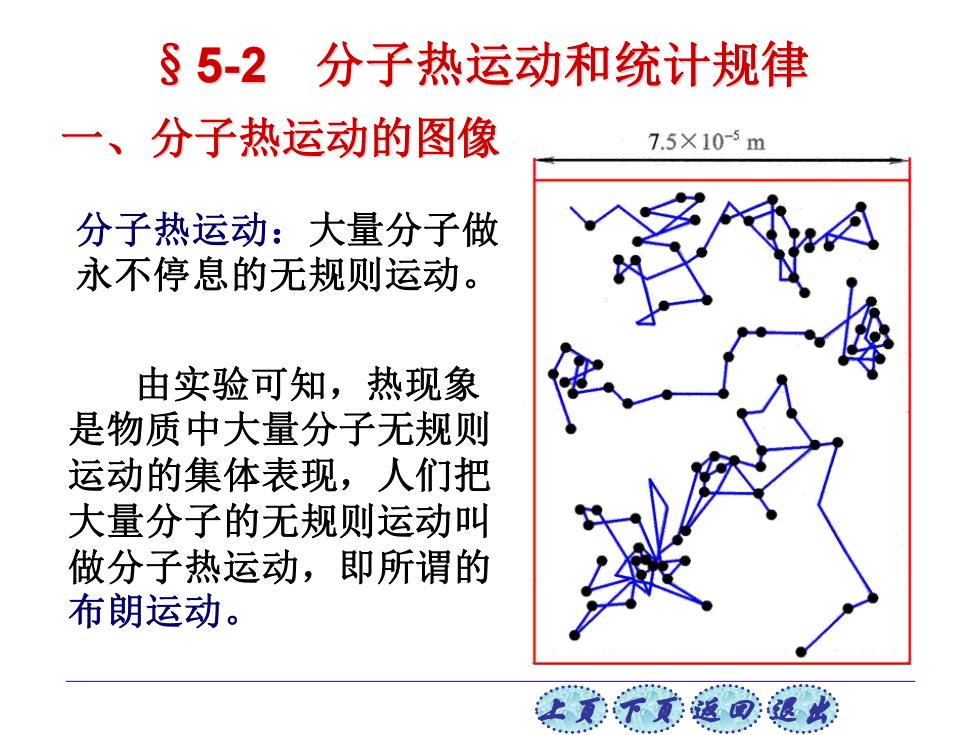
§5-2 分子热运动和统计规律 一、分子热运动的图像 7.5×10-5m 分子热运动:大量分子做 永不停息的无规则运动。 由实验可知,热现象 是物质中大量分子无规则 运动的集体表现,人们把 大量分子的无规则运动叫 做分子热运动,即所谓的 布朗运动。 让美下元返回:退欢
上页 下页 返回 退出 由实验可知,热现象 是物质中大量分子无规则 运动的集体表现,人们把 大量分子的无规则运动叫 做分子热运动,即所谓的 布朗运动。 分子热运动:大量分子做 永不停息的无规则运动。 一、分子热运动的图像 §5-2 分子热运动和统计规律

在标准状态下,对于同一物质气体的密度大约为 液体的1/1000。设液体分子是紧密排列的,则气体分 子之间的距离大约是分子本身线度(1010m)的 (1000)13倍,即10倍左右。所以把气体看作是彼此相 距很大间隔的分子集合。 在气体中,由于分子的分布相当稀疏,分子与分子 间的相互作用力,除了在碰撞的瞬间外,极其微小。 在连续两次碰撞之间分子所经历的路程平均为 10-7m,而分子的平均速率很大,约为500m/s。因此, 平均大约经过1010s,分子与分子碰撞一次,即在1s 内,一个分子将受到100次碰撞。分子碰撞的瞬间大 约是10-12s,这一时间远小于分子自由运动所经历的平 均时间(10-10s)。因此,在分子的连续两次碰撞之间, 分子的运动可看作由其惯性支配的自由运动。 让意了文道回退此
上页 下页 返回 退出 在标准状态下,对于同一物质气体的密度大约为 液体的1/1000。设液体分子是紧密排列的,则气体分 子之间的距离大约是分子本身线度(10-10 m) 的 (1000) 1/3倍,即10倍左右。所以把气体看作是彼此相 距很大间隔的分子集合。 在连续两次碰撞之间分子所经历的路程平均为 10-7 m,而分子的平均速率很大,约为500 m/s。因此, 平均大约经过10-10s,分子与分子碰撞一次,即在1s 内,一个分子将受到1010次碰撞。分子碰撞的瞬间大 约是10-12 s,这一时间远小于分子自由运动所经历的平 均时间(10-10s)。因此,在分子的连续两次碰撞之间, 分子的运动可看作由其惯性支配的自由运动。 在气体中,由于分子的分布相当稀疏,分子与分子 间的相互作用力,除了在碰撞的瞬间外,极其微小

二、分子热运动的基本特征 分子热运动的基本特征是永恒的运动与频繁 的相互碰撞。它与机械运动有本质的区别,故不 能简单应用力学定律来解决分子热运动问题。 1.无序性 某个分子的运动,是杂乱无章的,无序的; 各个分子之间的运动也不相同,即无序性;这正 是热运动与机械运动的本质区别。 让美下觉返司速此
上页 下页 返回 退出 分子热运动的基本特征是永恒的运动与频繁 的相互碰撞。它与机械运动有本质的区别,故不 能简单应用力学定律来解决分子热运动问题。 1.无序性 某个分子的运动,是杂乱无章的,无序的; 各个分子之间的运动也不相同,即无序性;这正 是热运动与机械运动的本质区别。 二、分子热运动的基本特征

2.统计性 但从大量分子的整体的角度看,存在一定 的统计规律,即统计性。 例如: 在平衡态下,气体分子的空间分布(密度) 是均匀的。(分子运动是永恒的) 可作假设:气体分子向各个方向运动的机会 是均等的,或者说沿各个方向运动的平均分子数 应相等且分子速度在各个方向的分量的统计平均 值也相等。 对大量分子体系的热平衡态,它是成立的
上页 下页 返回 退出 2.统计性 但从大量分子的整体的角度看,存在一定 的统计规律,即统计性。 例如: 在平衡态下,气体分子的空间分布(密度) 是均匀的。(分子运动是永恒的) 可作假设:气体分子向各个方向运动的机会 是均等的,或者说沿各个方向运动的平均分子数 应相等且分子速度在各个方向的分量的统计平均 值也相等。 对大量分子体系的热平衡态,它是成立的

3.统计方法 分子热运动具有无序性与统计性,与机械运动有 本质的区别,故不能简单应用力学定律来解决分子热 运动问题。必须兼顾两种特征,应用统计方法。 气体动理论中,求出大量分子的某些微观量的统 计平均值,用它来解释实验中测的宏观量,故可从实 测的宏观量了解个别分子的真实性质。 统计方法同时伴随着起伏现象。 如对气体中某体积内的质量密度的多次测量,各 次测量对平均值都有微小的偏差。当气体分子数很大 时,起伏极微小,完全可忽略;当气体分子数较小时, 起伏与平均值可比拟,不可忽略。故统计规律只适用 于大量分子的整体。 让美下元返回退欢
上页 下页 返回 退出 分子热运动具有无序性与统计性,与机械运动有 本质的区别,故不能简单应用力学定律来解决分子热 运动问题。必须兼顾两种特征,应用统计方法。 3.统计方法 气体动理论中,求出大量分子的某些微观量的统 计平均值,用它来解释实验中测的宏观量,故可从实 测的宏观量了解个别分子的真实性质。 统计方法同时伴随着起伏现象。 如对气体中某体积内的质量密度的多次测量,各 次测量对平均值都有微小的偏差。当气体分子数很大 时,起伏极微小,完全可忽略;当气体分子数较小时, 起伏与平均值可比拟,不可忽略。故统计规律只适用 于大量分子的整体