《复变函数与积分变换》课程教学资源（PPT课件）第八章 傅里叶变换（Fourier变换）

复变函数()e-o d则=CnTT2C二-jon dt fr fa(t)e-jon dte二J-14.432111jone-jont-jonee-4j0,4j0-1Y1一sin0nsinc(のn) (n = 0,±1,±2, ...二220nU

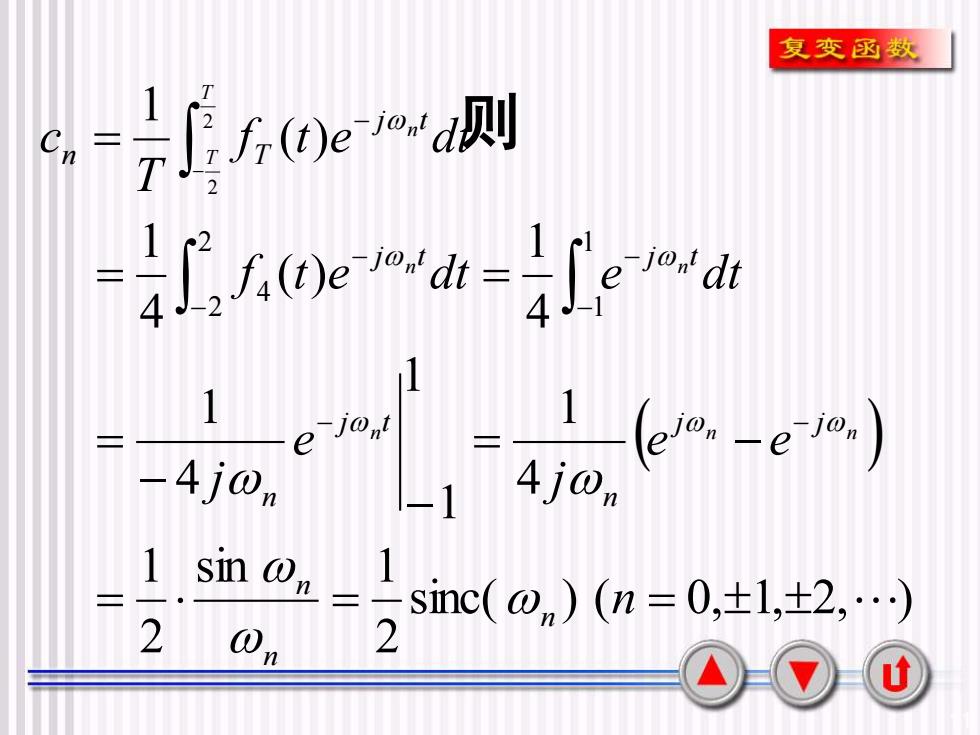
11 则 ( ) sinc( ) ( 0, 1, 2, ) 2 sin 1 2 1 4 1 1 1 4 1 4 1 ( ) 4 1 ( ) 1 1 1 2 2 4 2 2 =  = =    = − − − = = = = − − − − − − −   − n e e j e j f t e dt e dt f t e dt T c n n n j j n j t n j t j t j t n T n n n n n T T n           

复变函数Sinc函数定义为sincSinc涵数介绍xsin x严格讲函数在x =0处是无定义的,但是因为lim=1x-0xsinx所以定义sinc(O)=1,用不严格的形式就写作= 1,xIx=0则函数在整人实轴连续sinc(x)u

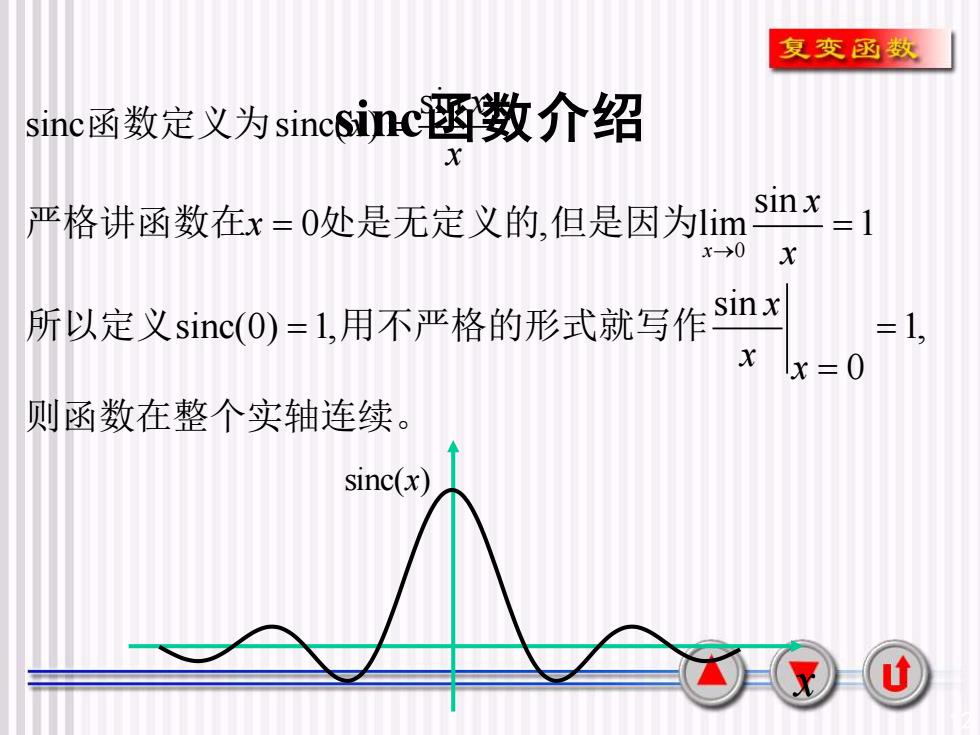
12 sinc函数介绍 0 sin sinc sinc( ) sin 0 , lim 1 sin sinc(0) 1, 1, 0 x x x x x x x x x x → = = = = = = 函数定义为 严格讲函数在 处是无定义的 但是因为 所以定义 用不严格的形式就写作 则函数在整个实轴连续。 sinc(x) x

复变函数sinc(の）（前面计算出C二一n22元n元可将c,以竖线标在频率图上0=n@=n2T0山

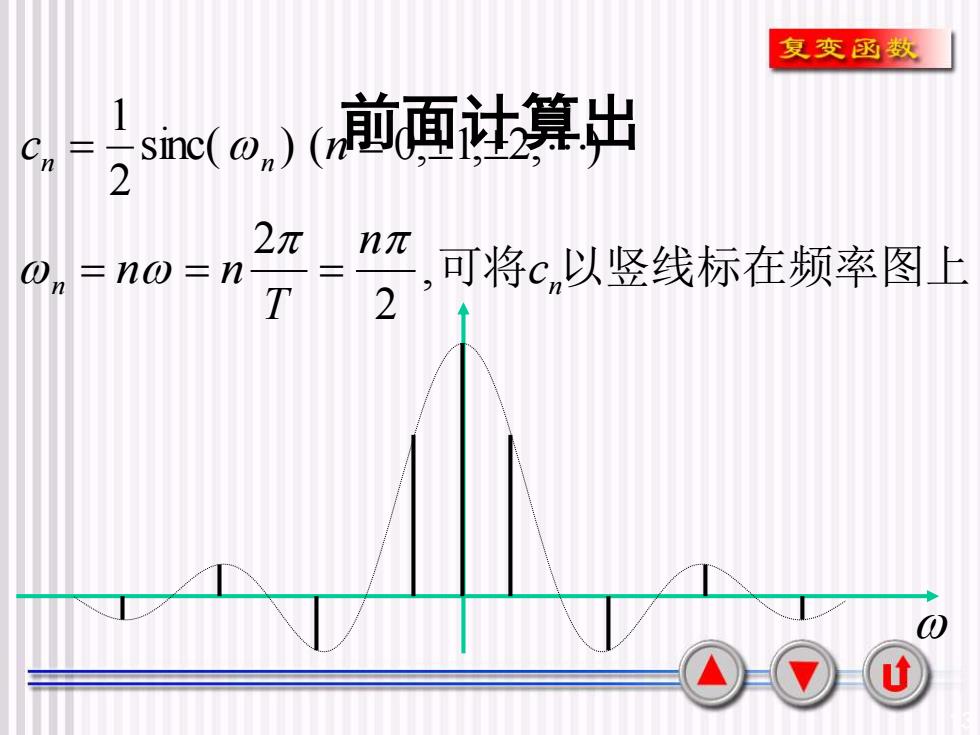
13 前面计算出 n 可将 n 以竖线标在频率图上 n n c n T n n c n , 2 2 sinc( ) ( 0, 1, 2, ) 2 1      = = = = =    

现在将周期扩大一倍，令T=8以t)为基础构造一周期为8的周期函数f:(t)f8Zf(t +8n),f.(t) =n=-82元2元元n元0n=nの =-T4.84fs(t)7-1uT=8

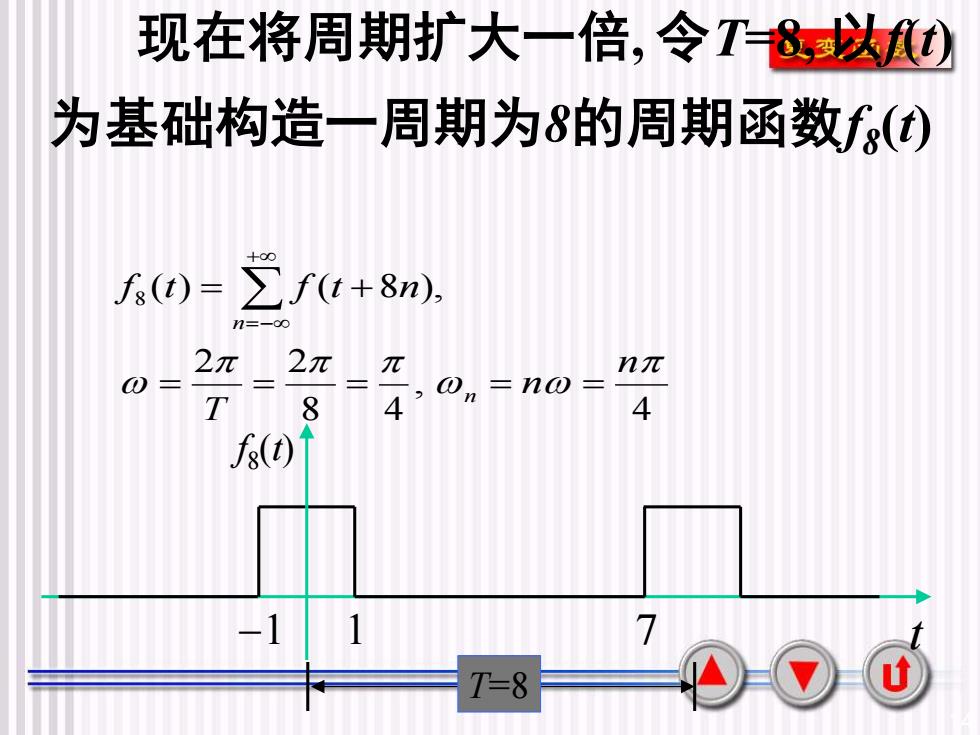
14 现在将周期扩大一倍, 令T=8, 以f(t) 为基础构造一周期为8的周期函数f8 (t) 4 , 8 4 2 2 ( ) ( 8 ), 8        n n T f t f t n n n = = = = = =  + + =− −1 1 7 T=8 f8 (t) t

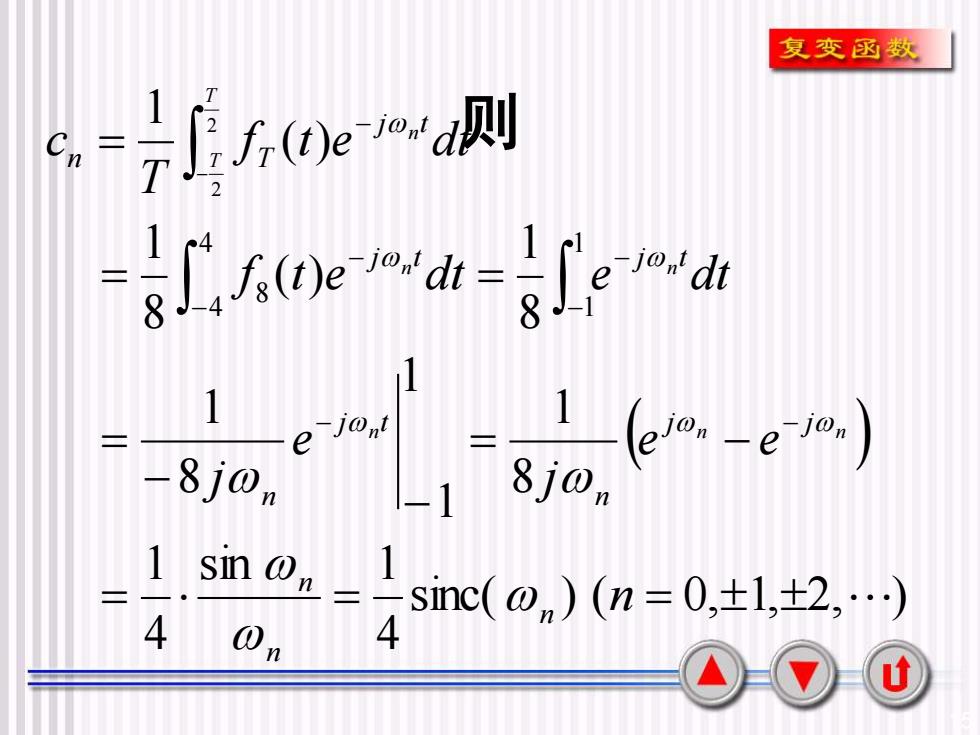
复变函数fr(t)e-jo' d则Ca=WCC1-jon dte二J-1811e-jontlejone-jon8j0,8j0,/-1n1sin0nsinc(のn) (n = 0,±1,±2,...)一440nu

15 则 ( ) sinc( ) ( 0, 1, 2, ) 4 sin 1 4 1 8 1 1 1 8 1 8 1 ( ) 8 1 ( ) 1 1 1 4 4 8 2 2 =  = =    = − − − = = = = − − − − − − −   − n e e j e j f t e dt e dt f t e dt T c n n n j j n j t n j t j t j t n T n n n n n T T n           