《复变函数与积分变换》课程教学资源（PPT课件）第八章 傅里叶变换（Fourier变换）

级数化为：复变函数inot-inotinot-inot0e+eeeeao +Z+b,ann222in=l8-ib+ibana.ao2ninotn-inotnn++ee222n=l-ibn +ibanaoann则 co =元["T/2 -(1)dt令CodC-nn222Cf()[eosno -sio dt=(red([ot +ii]dt=(emd(n=1.2..)(c n=c)U

6    = −  = − −       + + − = +         − + + + 1 0 1 0 2 2 2 2 2 2 n n n i n t n n i n t n i n t i n t n i n t i n t n e a ib e a a ib i e e b e e a a       级数化为：     ( ) 2 0 0 0 2 2 2 2 2 2 2 2 2 1 , , , ( ) 2 2 2 1 1 ( ) cos sin ( ) 1 1 ( ) cos sin ( ) 1,2, ( ) T n n n n n n T T T T in t n T T T T T T in t n T T n T T n n a a ib a ib c c d c f t dt T c f t n t i n t dt f t e dt T T d f t n t i n t dt f t e dt c T T n c c       − − − − − − − − − + = = = = = − = = + =  = =      令 则

复变函数?1/2合并为：C,=六[T/2 fr(t)e-inor dt (n = 0,±1,+2,.-T/2+8·T/2ZinotZleinoto-inot dt级数化为fr(t)eeC.11-T/2鑫n-T/2Tn=-80cn=F(nの)一J-(t)的离散频谱;Cnf-(t)的离散振幅频谱;argcn一Jr(t)的离散相位频谱；n E Z.若以f (t)描述某种信号，则c,可以刻画 f-(t)的频率特征。u

7 ( ) 2 2 1 ( ) 0, 1, 2, T in t n T T c f t e dt n T −  − = =   合并为：  2 2 1 ( ) T in t in in t n T T n n c e f e d e T      + + − − =− =−   =       级数化为：  c F n n = ( ) T ( ) n f t c 的离散频谱； ( ) arg T n f t c 的离散振幅频谱； ( ) . T f t n 的离散相位频谱；   若以f t c f t T n T ( )描述某种信号，则 可以刻画 ( )的 频率特征

XTJ双T复变函数化而来的作周期为T的函数f(t),使其在[T/2,T/2]之内等于f(t),在[-T/2,T/2]之外按周期T延拓到整个数轴上，则T越大f(t)与f(t)相等的范围也越大,这就说明当T→>时周期函数f(t)便可转化为f(t),T-→+8即有U

8 看成是由某个周期函数fT (t)当T→时转 化而来的. 作周期为T的函数fT (t), 使其在[− T/2,T/2]之内等于f (t), 在[−T/2,T/2]之外 按周期T延拓到整个数轴上, 则T越大, fT (t)与f (t)相等的范围也越大, 这就说明 当T→时, 周期函数fT (t)便可转化为f (t), 即有 lim ( ) ( ) T T f t f t →+ =

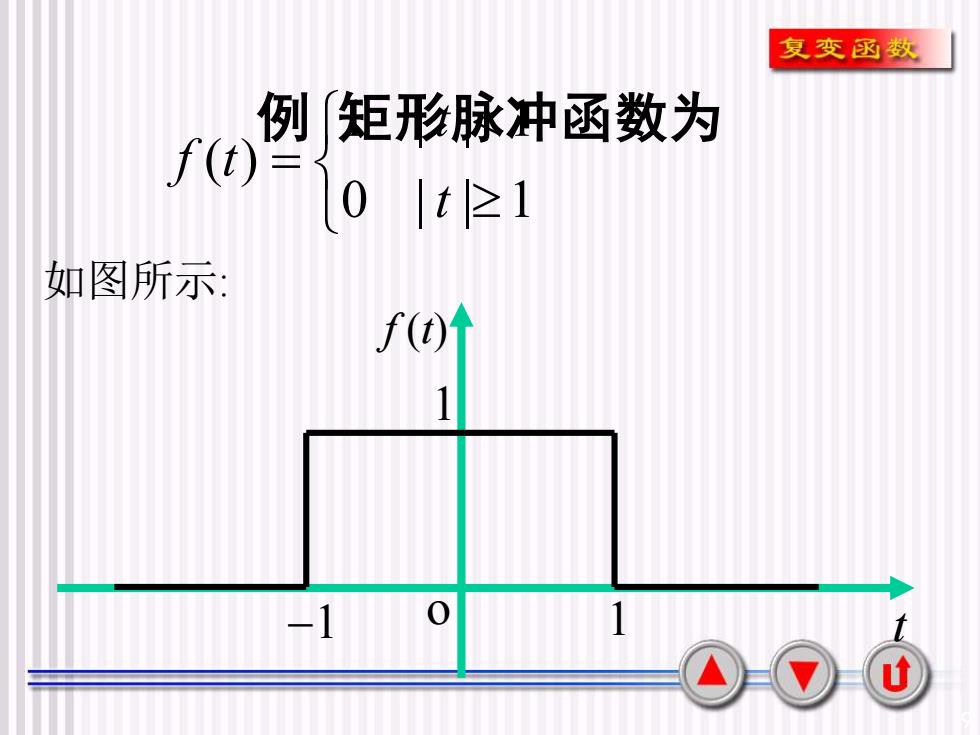
复变函数例「矩形脉冲函数为f(t)01t ≥1如图所示：f(t)0-1u

9 例 矩形脉冲函数为 1 | | 1 ( ) 0 | | 1 t f t t   =    如图所示: −1 o 1 t f (t) 1

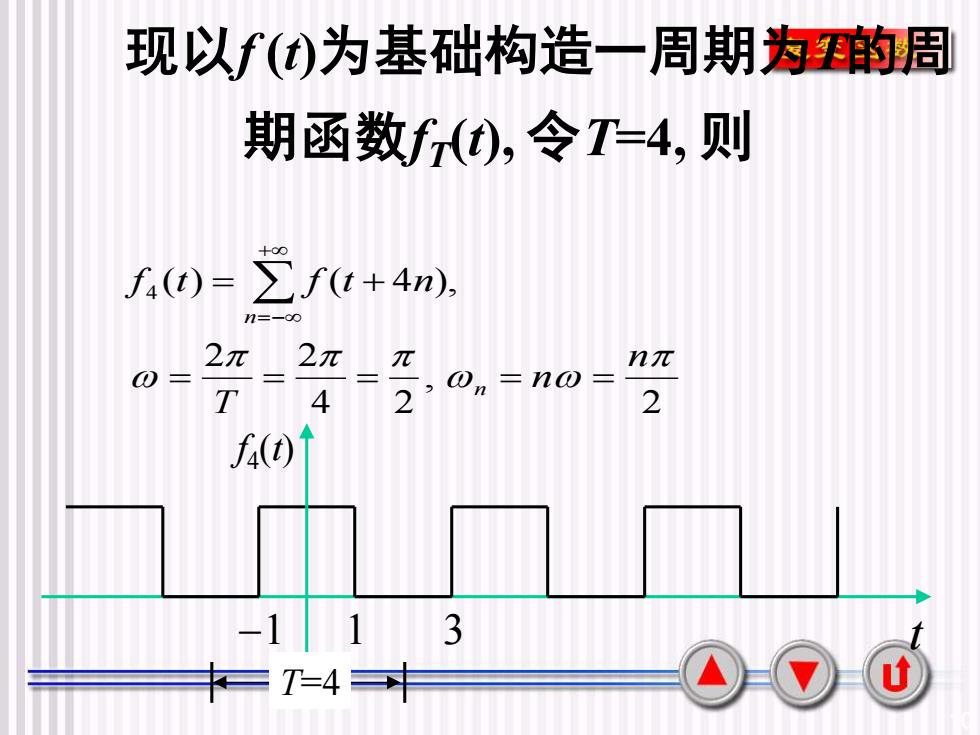
现以f(t)为基础构造一周期为T的周期函数f(t),令T=4,则+8Z f(t + 4n),f4(t) =n=-802元2元元n元00=n-n2T42f(t)3-1UT=4

10 现以f (t)为基础构造一周期为T的周 期函数fT (t), 令T=4, 则 2 , 4 2 2 2 ( ) ( 4 ), 4        n n T f t f t n n n = = = = = =  + + =− −1 1 3 T=4 f4 (t) t