《复变函数与积分变换》课程教学资源（PPT课件）第八章 傅里叶变换（Fourier变换）

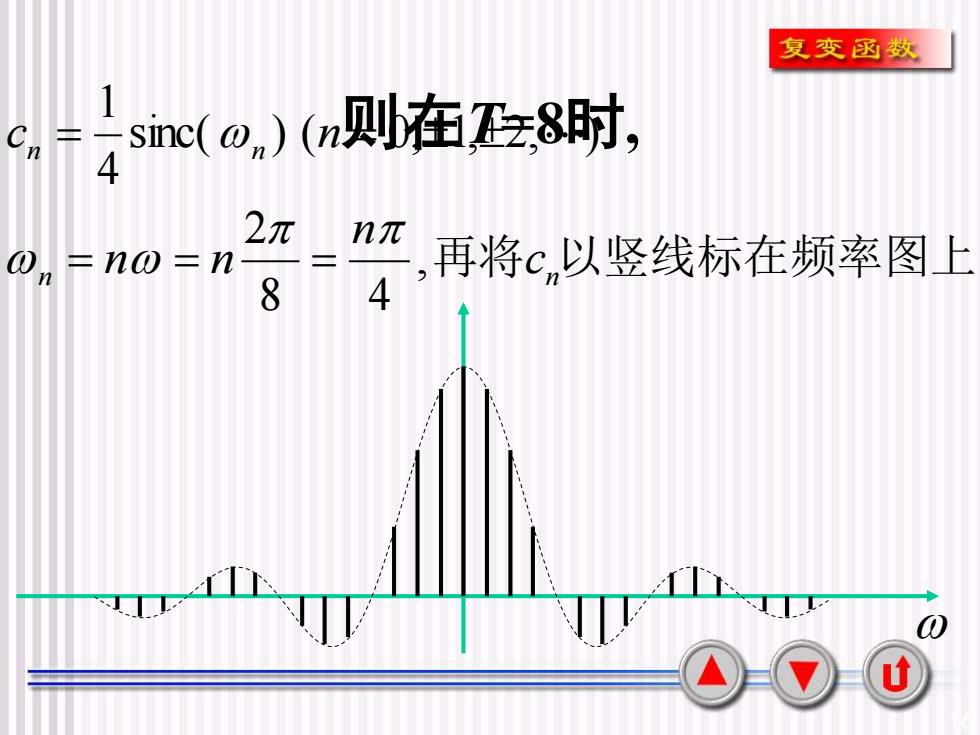
复变函数sinc(のn）（n则在z,8时C二-n42元n元再将c,以竖线标在频率图上0=nの=n840u

16 则在T=8时, n 再将 n 以竖线标在频率图上 n n c n n n c n , 8 4 2 sinc( ) ( 0, 1, 2, ) 4 1      = = = = =    

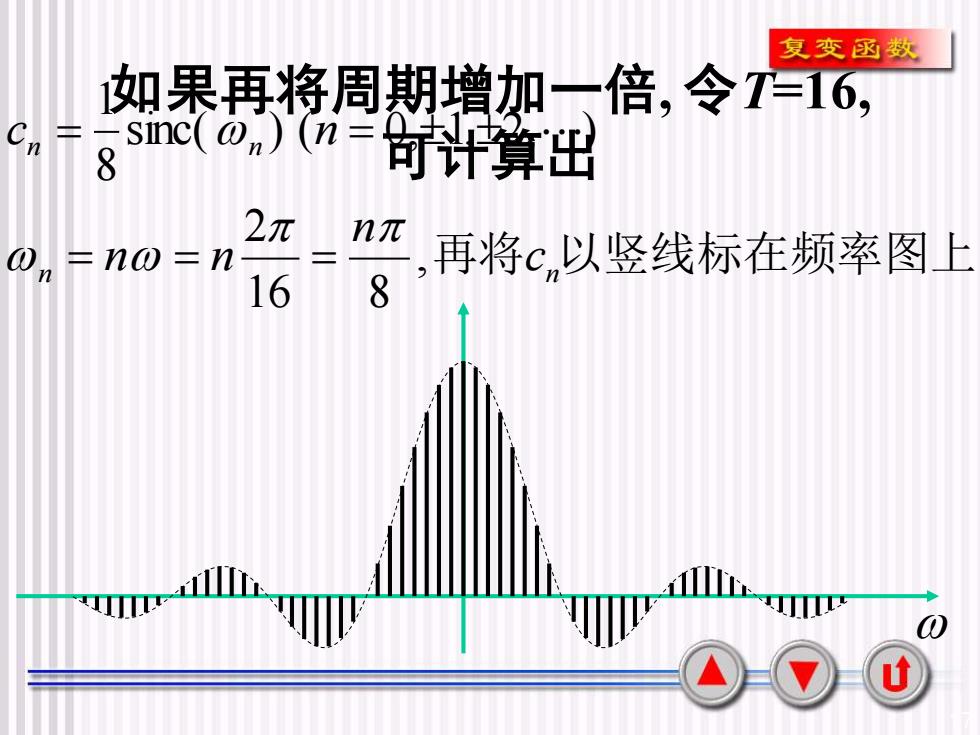
复变函数如果再将周期增加一倍，令T-16,C= sinc(on)(n =白二句计算出n82元n元再将c.以竖线标在频率图上0=nの=n8160u

17 如果再将周期增加一倍, 令T=16, 可计算出 n 再将 n 以竖线标在频率图上 n n c n n n c n , 16 8 2 sinc( ) ( 0, 1, 2, ) 8 1      = = = = =    

复变函数12f,()般地t对于周期T一二CM7T12-jon dte111-jont(ejo,e-joneTjOnTjo一1-1n22sin0nsinc(のn) (n = 0,±1,±2,:.TT0nu

18 一般地, 对于周期T ( ) sinc( ) ( 0, 1, 2, ) 2 sin 2 1 1 1 1 1 ( ) 1 1 1 2 2 =  = =    = − − − = = = − − − − −  − n T T e e Tj e Tj e dt T f t e dt T c n n n j j n j t n j t j t n T n n n n T T n          

弦波的频率间隔越来越小，而它们的强度在各个频率的轮廓则总是sinc函数的形状,因此,如果将方波函数f(t)看作是周期无穷大的周期函数，则它也可以看作是由无穷多个无穷小的正弦波构成将那个频率上的轮廓即sinc函数的形状看作是方波函数f(t)的各个频率成份上的分布，称作方波函数f()的傅里叶变换

19 当周期T越来越大时, 各个频率的正 弦波的频率间隔越来越小, 而它们的强 度在各个频率的轮廓则总是sinc函数的 形状, 因此, 如果将方波函数f (t)看作是 周期无穷大的周期函数, 则它也可以看 作是由无穷多个无穷小的正弦波构成, 将那个频率上的轮廓即sinc函数的形状 看作是方波函数f (t)的各个频率成份上 的分布, 称作方波函数f (t)的傅里叶变换

1.2 Fourier积分公式与Fourier积分存在良理函数I.设f-(t)为T-周期函数，在上满足Dirichlet条件2'2则f(t)可展开为Fourier级数：+8+8Ziont之inotf(t) =Chei二eC.nn=-80n=-αCT/2fr (t)e-io,' dtOn= nO = 2n元/T, Cn-T12f(t)e-jo,t dt lejo,t即f(t)=-7T2由 lim f(t)= f(t)u

20 2 2 ( ) , Dirichlet , 2 2 ( ) Fourier ( ) , 1 2 , ( ) n n T T in t i t T n n n n T i t n n T T T T f t T f t f t c e c e n n T c f t e dt T       + + =− =− − −   − −    = = = = =    设 为 周期函数，在 上满足 条件 则 可展开为 级数: 2 2 1 j j ( ) ( ) d . T n n T t T T n f t f e e T      − + − =−   =     即   lim ( ) ( ) T T f t f t →+ 由 = 1.2 Fourier积分公式与Fourier积分存在定理