
7.3行列式的定义和计算 两种定义方法: ·1。按全排列求和定义, a11 全排列 D= ∑(-l)'apa2pn…ap. aml amn 其中t为第种排列的逆序数
7.3 行列式的定义和计算 两种定义方法: • 1。按全排列求和定义, 其中t j为第j种排列的逆序数。 1 2 11 1 1 2 1 ( 1) j n n t p p np j m mn a a D a a a a a = = − 全排列

行列式第2种定义方法 2。按解的分母项,从低阶到高阶用归纳法定义 二阶: a12 det()= a411 a11a22-a21a12 a21 a22 三阶: det(A)=a. a22a23 a2123 a12 +a13 a21a22 a32a33 a31a33 a31a32 =(-l)2a1·det(M)+(-l)3a2·det(M12)+(-l)4a3·detM13) -)a,day)
行列式第2种定义方法 2。按解的分母项,从低阶到高阶用归纳法定义 二阶: 三阶: 11 12 11 22 21 12 21 22 det( ) a a A a a a a a a = = − 22 23 21 23 21 22 11 12 13 32 33 31 33 31 32 2 3 4 11 11 12 12 13 13 3 1 1 1 1 det( ) ( 1) det( ) ( 1) det( ) ( 1) det( ) ( 1) det( ) j j j j a a a a a a A a a a a a a a a a a M a M a M a M + = = − + = − + − + − = −

两种定义方法的比较 第一种定义的两个数学难点‘全排列'和‘逆序 数’,是绝大多数工科学生一生不会用的。 第二种定义方法自然地得出了行列式按行(或按列) 展开的公式。美国教材都用第二种定义方法,成 电教材(全国精品课程)也用这种方法。 ·两种方法都不能用来计算,因为其计算效率都极 低,25×25矩阵要算上万年。 第8章将指出,行列式的几何意义是面积或体积,可 否从这方面探索,因为它的用途很单一,就是判 断奇异性,连正负号都不必关心
两种定义方法的比较 第一种定义的两个数学难点‘全排列’和‘逆序 数’,是绝大多数工科学生一生不会用的。 第二种定义方法自然地得出了行列式按行(或按列) 展开的公式。美国教材都用第二种定义方法,成 电教材(全国精品课程)也用这种方法。 • 两种方法都不能用来计算,因为其计算效率都极 低,25×25矩阵要算上万年。 第8章将指出,行列式的几何意义是面积或体积,可 否从这方面探索,因为它的用途很单一,就是判 断奇异性,连正负号都不必关心

行列式的计算方法 ·计算行列式的最好方法还是行阶梯法,可 以利用u分解 [L,U]=lu(A) 把A分解为一个准下三角矩阵L和一个上三角 矩阵U的乘积。因为det(L)=1,所以U和A的 行列式相等。det(A)=det(U) 而三角矩阵U的det(U)很好求。只要把U的主 对角线元素连乘就可得到它的行列式。 此法所需的乘法次数仅为定义1法的1023
行列式的计算方法 • 计算行列式的最好方法还是行阶梯法,可 以利用lu分解 [L,U]=lu(A) 把A分解为一个准下三角矩阵L和一个上三角 矩阵U的乘积。因为det(L)=1,所以U和A的 行列式相等。 det(A)= det(U) 而三角矩阵U的det(U)很好求。只要把U的主 对角线元素连乘就可得到它的行列式。 此法所需的乘法次数仅为定义1法的10 -23
行列式计算实例7.3.1 ·程序如下 10 8 1 2 5 6 4 [l,u]=u(A), A= 6 0 8 du diag(u) 5 8 4 0 D=prod(du) 9 4 2 9 1 结果为 。 du=10 -4.810.625 9.4824-1.2349 D=5.9720e+003=5972
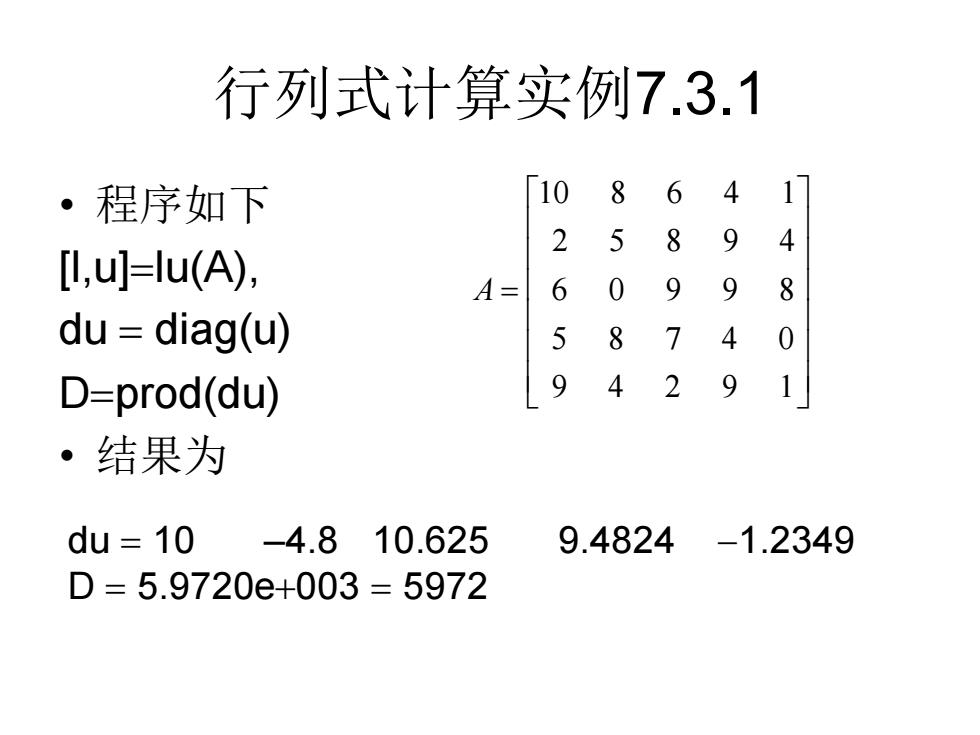
行列式计算实例7.3.1 • 程序如下 [l,u]=lu(A), du = diag(u) D=prod(du) • 结果为 10 8 6 4 1 2 5 8 9 4 6 0 9 9 8 5 8 7 4 0 9 4 2 9 1 A = du = 10 –4.8 10.625 9.4824 −1.2349 D = 5.9720e+003 = 5972