
例5 已知X~W4,o2),求P0X-4Kk),其中k=1,2,3,4,5,6 解PIX-严K)=Pu-ko<X<u+ko) 6 =Φ(k)-Φ(-k) =Φ(k)-[1-Φ(k)]=2Φ(k)-1 所以,所求概率依次为: P0X-4K1)=2Φ0)-1=0.6826 P0X-4K2)=2(2)-1=0.954 X=4K3)=2Φ(3)-1=0.9973 P0X-LK4=24-1=0.9994 P1Y-Lk5=206-=1-0994 P1X-4K6)=206-1=0.9999998 在质量控制中,k=3时的情形特别有用。它告诉我们,如果质量 特性值X服从参数为和的正态分布,那么,它落在区间内的概率 高达99.73%;相反,落在区间之外(即)的概率只有0.27%。 这就是众所周知的“”原理。根据“”原理,如果发现质量特性 值X的观测结果不在区间内,就有合乎逻辑的理由怀疑生产过程 已经失控,面临的质量波动是由系统性的不良因素引起的。因为 在这种情况下,生产过程仍然正常的可能性只有0.27%,而己失 常的可能性却高达99.73%
例5 已知 , 求 ,其中 。 解 所以,所求概率依次为: • 在质量控制中,k=3时的情形特别有用。它告诉我们,如果质量 特性值X服从参数为和的正态分布,那么,它落在区间内的概率 高达99.73%;相反,落在区间之外(即)的概率只有0.27%。 这就是众所周知的“”原理。根据“”原理,如果发现质量特性 值X的观测结果不在区间内,就有合乎逻辑的理由怀疑生产过程 已经失控,面临的质量波动是由系统性的不良因素引起的。因为 在这种情况下,生产过程仍然正常的可能性只有0.27%,而已失 常的可能性却高达99.73%。 ~ ( , ) 2 X N (| | k) X P − k = 1,2,3,4,5,6 (| | ) ( ) k P k X k X P = − + − = (k) −(−k) = (k) −[1−(k)] = 2(k) −1 (| | 1) = 2(1) −1 = 0.6826 − X P (| | 2) = 2(2) −1 = 0.9544 − X P (| | 3) = 2(3) −1 = 0.9973 − X P (| | 4) = 2(4) −1 = 0.99994 − X P (| | 5) = 2(5) −1= 0.9999994 − X P (| | 6) = 2(6) −1 = 0.999999998 − X P
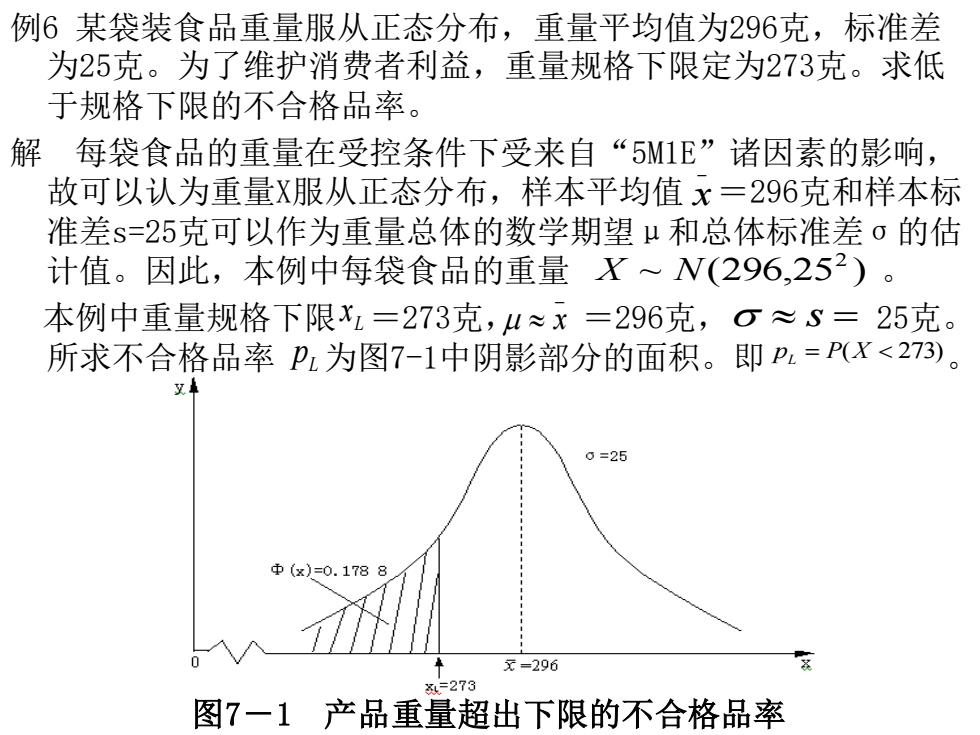
例6某袋装食品重量服从正态分布,重量平均值为296克,标准差 为25克。为了维护消费者利益,重量规格下限定为273克。求低 于规格下限的不合格品率。 解每袋食品的重量在受控条件下受来自“5M1E”诸因素的影响, 故可以认为重量X服从正态分布,样本平均值x=296克和样本标 准差s=25克可以作为重量总体的数学期望μ和总体标准差σ的估 计值。因此,本例中每袋食品的重量X~N(296,252)。 本例中重量规格下限xL=273克,u≈x=296克,O≈=25克。 所求不合格品率p为图7-1中阴影部分的面积。即P.=(x<273)。 0=25 中(x)=0.1788 元=296 =273 图7-1 产品重量超出下限的不合格品率
例6 某袋装食品重量服从正态分布,重量平均值为296克,标准差 为25克。为了维护消费者利益,重量规格下限定为273克。求低 于规格下限的不合格品率。 解 每袋食品的重量在受控条件下受来自“5M1E”诸因素的影响, 故可以认为重量X服从正态分布,样本平均值 =296克和样本标 准差s=25克可以作为重量总体的数学期望μ和总体标准差σ的估 计值。因此,本例中每袋食品的重量 。 本例中重量规格下限 =273克, =296克, 25克。 所求不合格品率 为图7-1中阴影部分的面积。即 。 _ x ~ (296,25 ) 2 X N L x _ x s = L p p = P(X 273) L 图7-1 产品重量超出下限的不合格品率