
第11章动量定理 §11-3质心运动定理和动量守恒 §11-4质心运动定理和动量守恒的应用
第11章 动量定理 §11-3 质心运动定理和动量守恒 §11-4 质心运动定理和动量守恒的应用

1.质点的动量:P=mV矢量,量纲为: kgm/s 2.质点的动量定理: ma= dv n dt d(mv)-Fdt 3.元冲量: dI=Fd t 矢量,量纲为:Ns I--Fadr 时间段内的冲量 mvz-mv =I dp=dl 为质点的动量定理的微分形式:
1.质点的动量: p=mv 矢量, 量纲为: kg m/s 2. 质点的动量定理: ma =F F v = dt d m d(mv ) = Fdt dp = dI 为质点的动量定理的微分形式. 3.元冲量: dI =F d t 矢量, 量纲为: N s = 2 1 t t I Fdt 时间段内的冲量 mv2 −mv1 =I
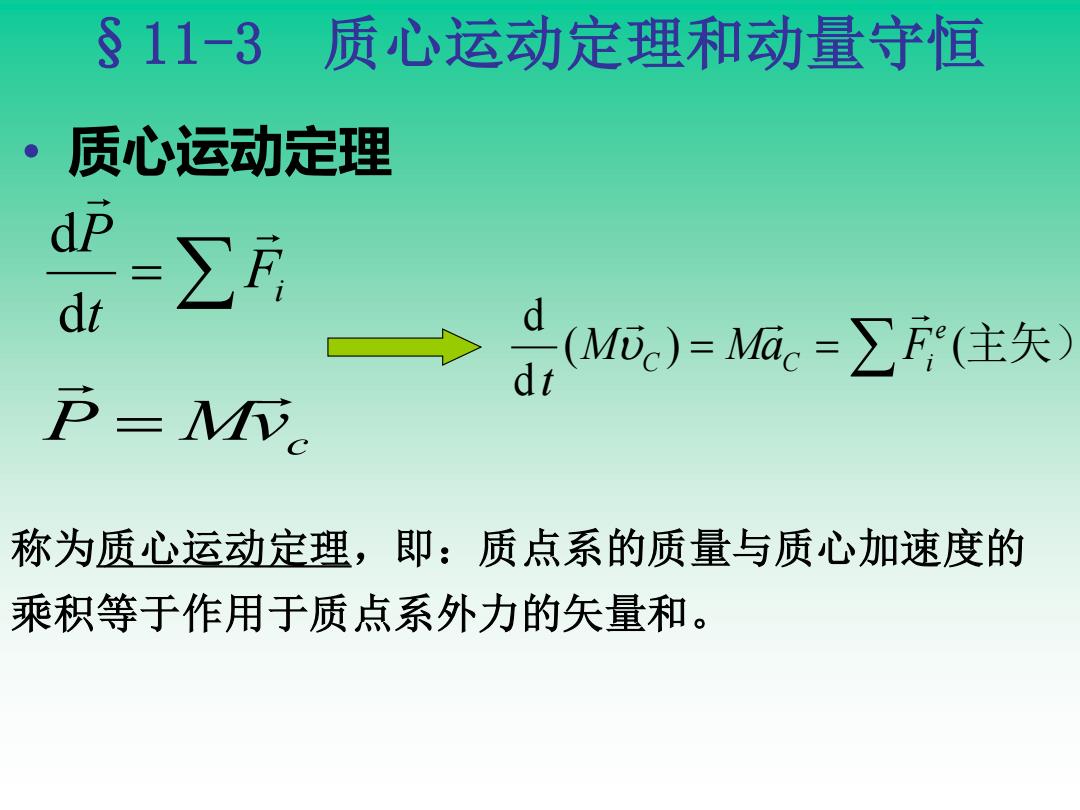
§11-3 质心运动定理和动量守恒 质心运动定理 =∑ (Mi,)=M6=∑F(住矢) P-MV 称为质心运动定理,即:质点系的质量与质心加速度的 乘积等于作用于质点系外力的矢量和
( ) (主矢) d d = = e C C Fi M Ma t 称为质心运动定理,即:质点系的质量与质心加速度的 乘积等于作用于质点系外力的矢量和。 P Mvc = = Fi t P d d • 质心运动定理 §11-3 质心运动定理和动量守恒

Ma。=∑F Max=∑F Mao,=∑F9 质心运动定理是动量定理的另一种表现形式,与质点运动 微分方程形式相似。对于任意一个质点系,无论它作什 么形式(平面运动)的运动,质心的运动定理描述是质 点系随基点平动的运动规律
= e MaC Fi = e Macx Fx = e Macy Fy 质心运动定理是动量定理的另一种表现形式,与质点运动 微分方程形式相似。对于任意一个质点系, 无论它作什 么形式(平面运动)的运动, 质心的运动定理描述是质 点系随基点平动的运动规律
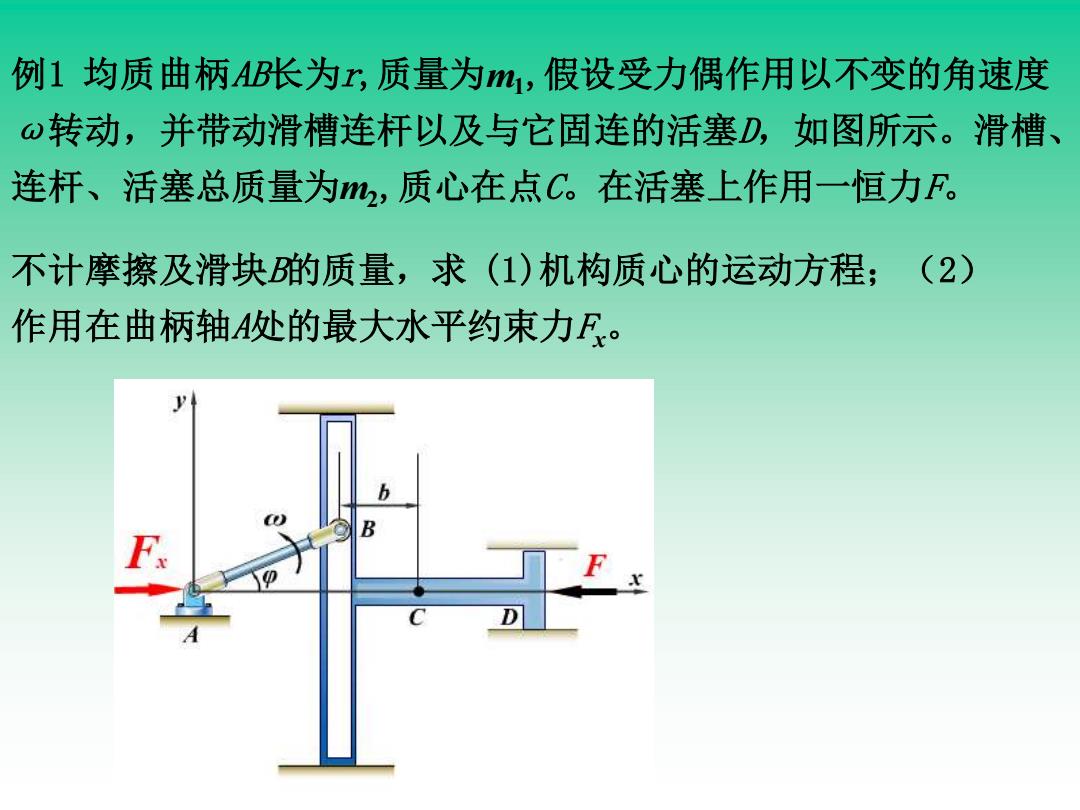
例1均质曲柄AB张为,质量为m,假设受力偶作用以不变的角速度 ⊙转动,并带动滑槽连杆以及与它固连的活塞D,如图所示。滑槽、 连杆、活塞总质量为m2,质心在点C。在活塞上作用一恒力F。 不计摩擦及滑块的质量,求(1)机构质心的运动方程;(2) 作用在曲柄轴A处的最大水平约束力F: 1
例1 均质曲柄AB长为r,质量为m1,假设受力偶作用以不变的角速度 ω转动,并带动滑槽连杆以及与它固连的活塞D,如图所示。滑槽、 连杆、活塞总质量为m2,质心在点C。在活塞上作用一恒力F。 不计摩擦及滑块B的质量,求 (1)机构质心的运动方程;(2) 作用在曲柄轴A处的最大水平约束力Fx