
第13章质点系动能定理 力的功 动能 动能定理与机械能守恒 功率、功率方程、机械效率 动力学普遍定理的综合应用 讨论
□ 力的功 □ 动能定理与机械能守恒 □ 功率、功率方程、机械效率 □ 讨论 □ 动能 第13章 质点系动能定理 □ 动力学普遍定理的综合应用

对点的动量矩: Lo=Mo(mv) 对轴的动量矩:Lz=Mz(mw) 动量矩定理: 立M.网 投影式: i dLs=ZM,(F) dt dL=ΣM,(oy d dL=ΣM(Fo
L M (mv) O = O L M (mv) Z = Z 对点的动量矩: 对轴的动量矩: 动量矩定理: = = n i O O M F dt dL 1 ( )
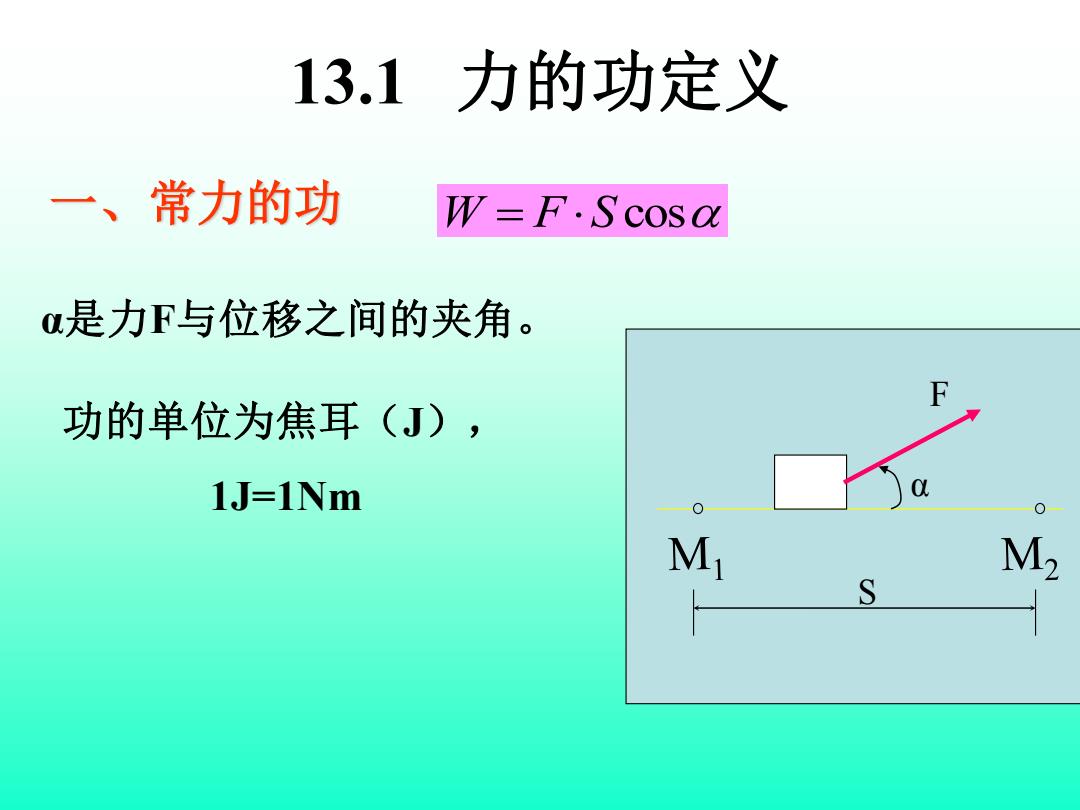
13. 1力的功定义 一、常力的功 W=F.Scosa α是力F与位移之间的夹角。 F 功的单位为焦耳(J), 1J=1Nm M M S
一、常力的功 F S α W = F S cos α是力F与位移之间的夹角。 功的单位为焦耳(J), 1J=1Nm 13.1 力的功定义
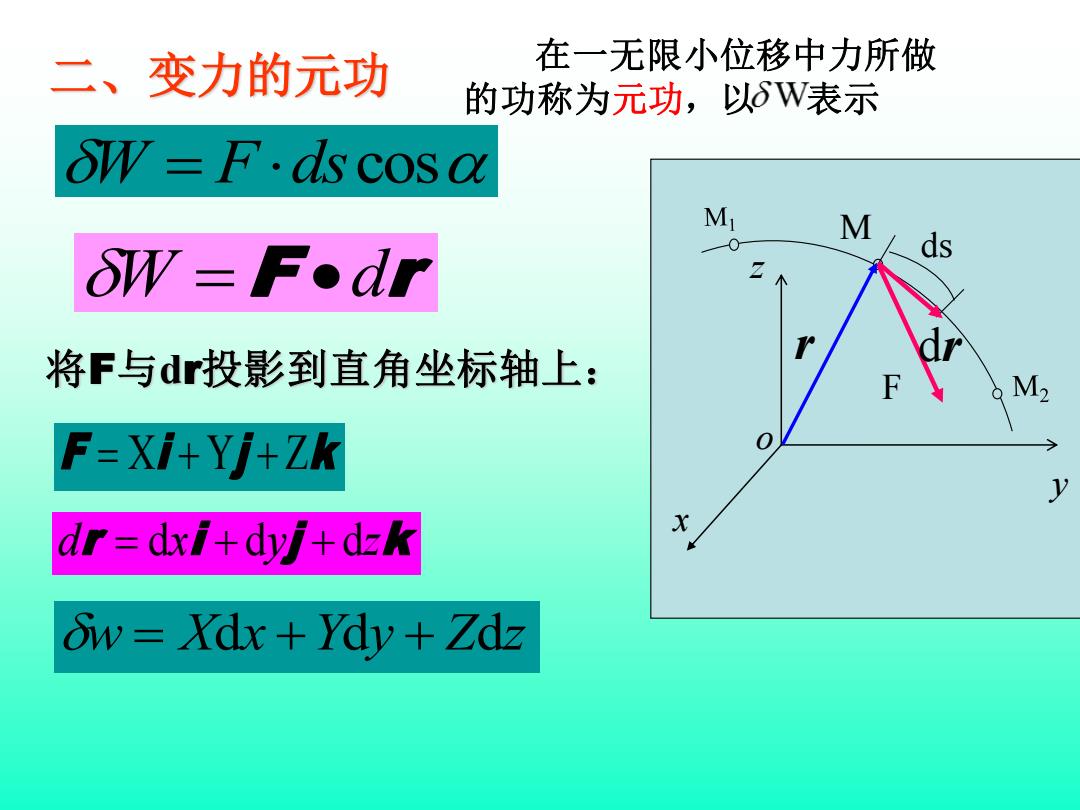
二、变力的元功 在一无限小位移中力所做 的功称为元功,以6W表示 δW=F.ds cos a M M δW=F●dr ds 将F与dr投影到直角坐标轴上: F F=Xi+Yj+Zk 0 y dr=dxi+dyj+dzk ow=Xdx+Ydy+Zdz
二、变力的元功 M F ds W = Fdscos dr W =F •dr y o x z r 将F与dr投影到直角坐标轴上: F = Xi + Yj + Zk dr = dxi + dyj + dzk w = Xdx +Ydy + Zdz 在一无限小位移中力所做 的功称为元功,以 表示

力F在曲线路程M,M中作功为 w=∫cos ads=∫F,ds M M M M1 ds (自然形式表达式) F M =「F.d (矢量式) 0 M y M2 Xdx+Ydy +Zd Mi (直角坐标表达式)
力 在曲线路程 中作功为 (自然形式表达式) (矢量式) (直角坐标表达式) M F ds dr y o x z r