解:如图所示研究整体系,建立坐标系如图 x.=∑x)y=∑m) M M y 曲柄AB的质心 cos p 2 r sin o 2 滑槽、连杆、活塞 X2c=rcoso+b 2c=0 mo+wowo6小nm+n m 质心运动方程 m +m
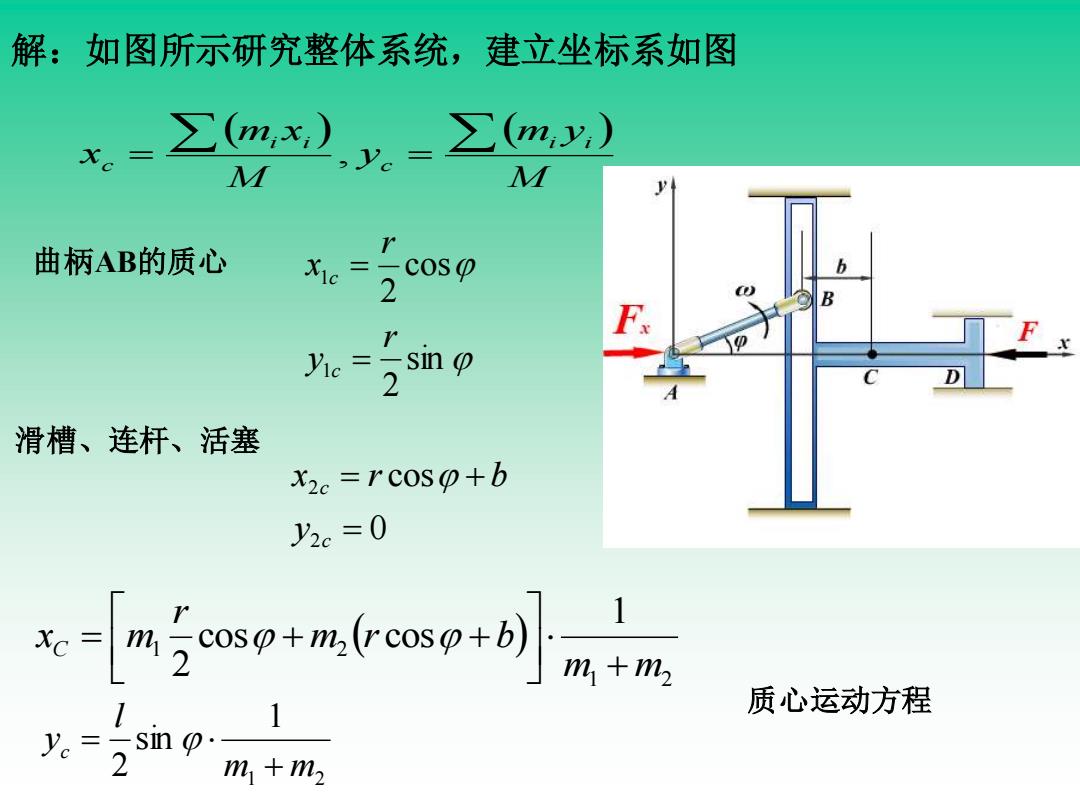
解:如图所示研究整体系统,建立坐标系如图 ( ) 1 2 1 2 1 cos cos 2 m m m r b r xC m + = + + ( ) ( ) M m y y M m x x i i c i i c = , = 曲柄AB的质心 sin 2 cos 2 1 1 r y r x c c = = 滑槽、连杆、活塞 0 cos 2 2 = = + c c y x r b 1 2 1 sin 2 m m l yc + = 质心运动方程
水平约束力 moong m.(ro) m +m d'xc _-ro"(n dt +%cos()) m,+m2(2 应用质心运动定理,解得 b rmcout 显然,最大水平约束力为 R=F+wf受+m
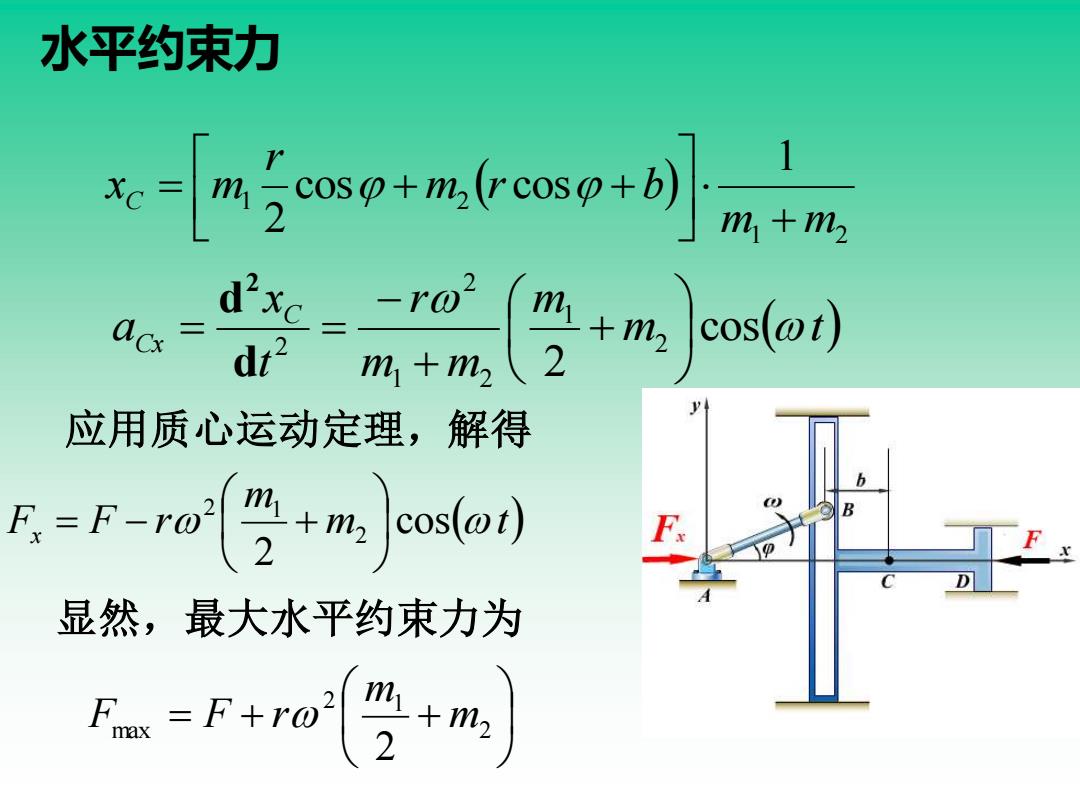
( ) 1 2 1 2 1 cos cos 2 m m m r b r xC m + = + + m ( t) m m m r t x a C Cx cos 2 2 1 1 2 2 2 + + − = = d d 2 应用质心运动定理,解得 m ( t) m F F r x cos 2 2 2 1 = − + 显然,最大水平约束力为 = + + 2 2 1 max 2 m m F F r 水平约束力
例2:己知定轮O、物A、B的质量为m、m4、m,若物 A以加速ā下降,不计动轮自重,求支座0的反力。 动力学的分析内容应从动力 学方程考虑。 动力学方程一边是受力状态; 一边是运动状态。所以,一 般的动力学问题应先分别考 虑受力、运动,再综合到动 力学方程中建立等式。 A mA B mB
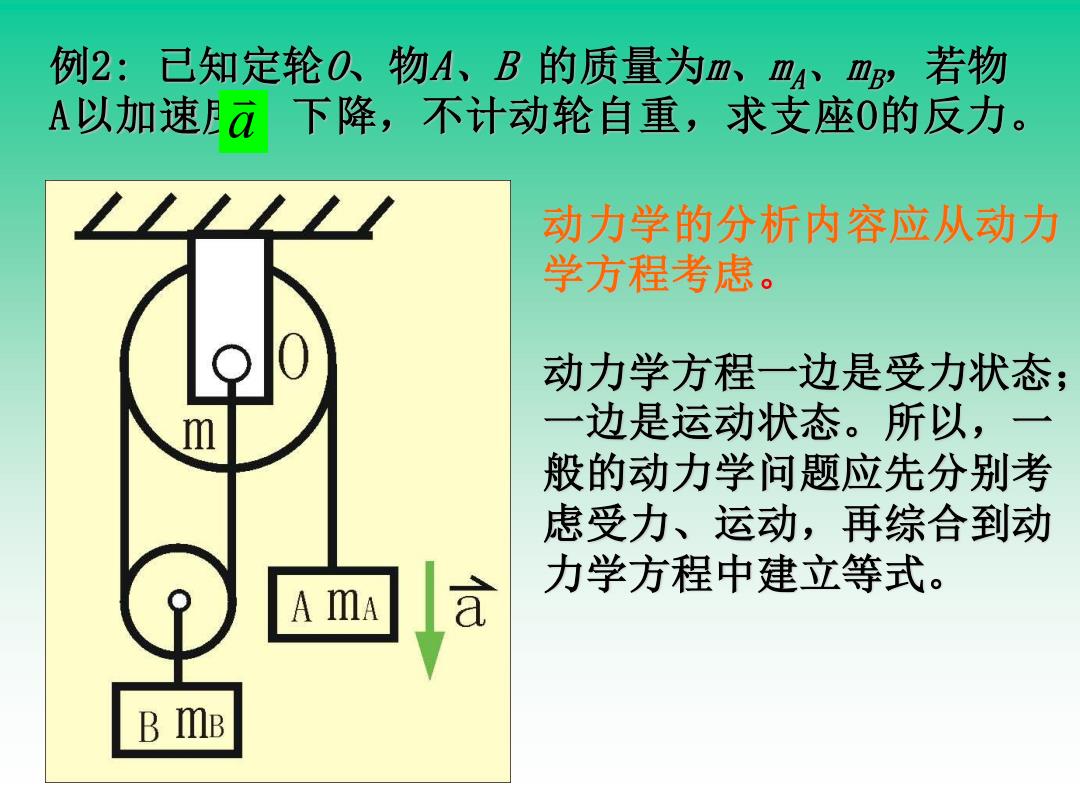
例2: 已知定轮O、物A、B 的质量为m、mA、mB,若物 A以加速度 下降,不计动轮自重,求支座O的反力。 动力学的分析内容应从动力 学方程考虑。 动力学方程一边是受力状态; 一边是运动状态。所以,一 般的动力学问题应先分别考 虑受力、运动,再综合到动 力学方程中建立等式。 a
一、受力分析 取“动轮一定轮一A一B”质点系为研究对象, 受力如图。 mg A mAg meg
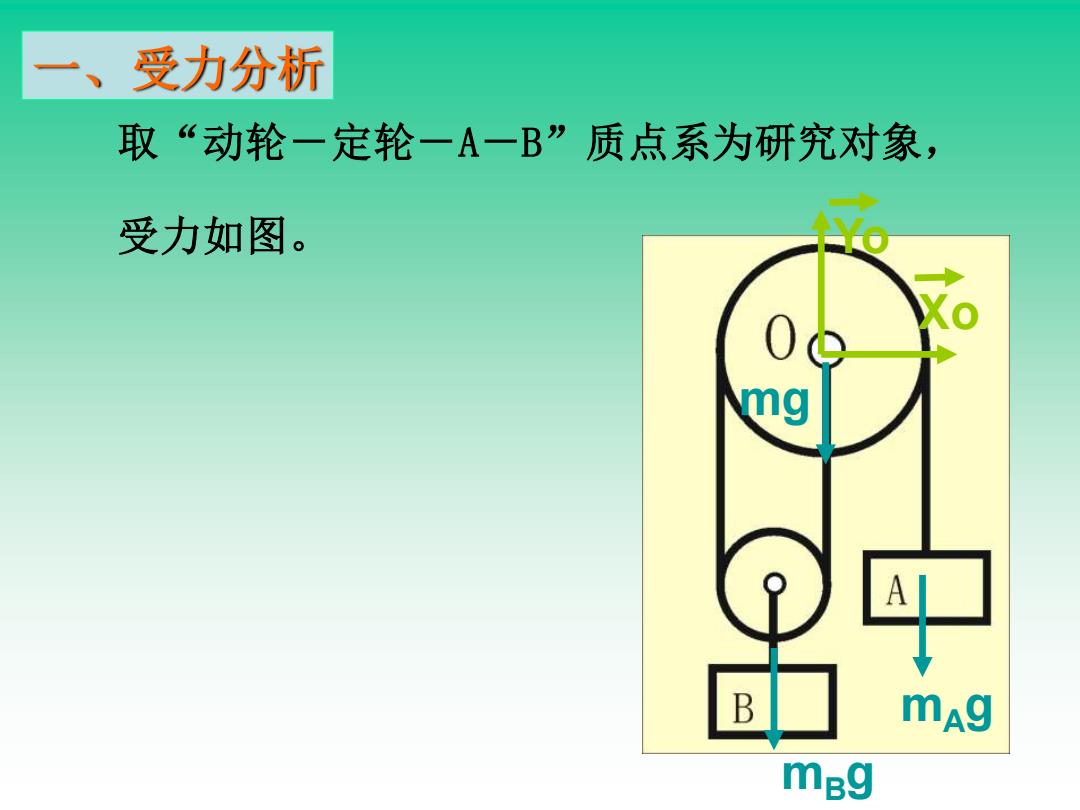
取“动轮-定轮-A-B”质点系为研究对象, 一、受力分析 Xo Yo mAg mg mBg 受力如图