
第6章↓ 点的运动学 ★矢量法 ★ 直角坐标法 ★ 自然(弧坐标)法 ★ 应用举例
第6章 点的运动学 ★ 矢量法 ★ 直角坐标法 ★ 自然(弧坐标)法 ★ 应用举例

§6-1 运动学的基本概念 非运动学:以几何观点(几何公理)研究物体的运 动(轨迹,速度和加速度),不考虑物体运动的原因. 固定参考系:一般采用固连于地球上的坐标系为 参考系,称为固定参考系。 参照物--参考体--参考坐标系---参考系 对任何物体运动的描述都是相对的。 +时间:瞬时和时间间隔 瞬时 时间间隔
运动学: 以几何观点(几何公理)研究物体的运 动(轨迹,速度和加速度), 不考虑物体运动的原因. §6-1 运动学的基本概念 固定参考系: 一般采用固连于地球上的坐标系为 参考系,称为固定参考系. 时间: 瞬时和时间间隔 瞬时 时间间隔 t1 t t2 t 参照物-----参考体------参考坐标系------参考系 对任何物体运动的描述都是相对的

点:就是指不计其形状、大小、只在空间占有确 定位置的几何点 刚体:可看作由无穷多个点的组成的不变形的几何 体。 直线运动 曲线运动
刚体:可看作由无穷多个点的组成的不变形的几何 体。 点:就是指不计其形状、大小、只在空间占有确 定位置的几何点 直线运动 曲线运动
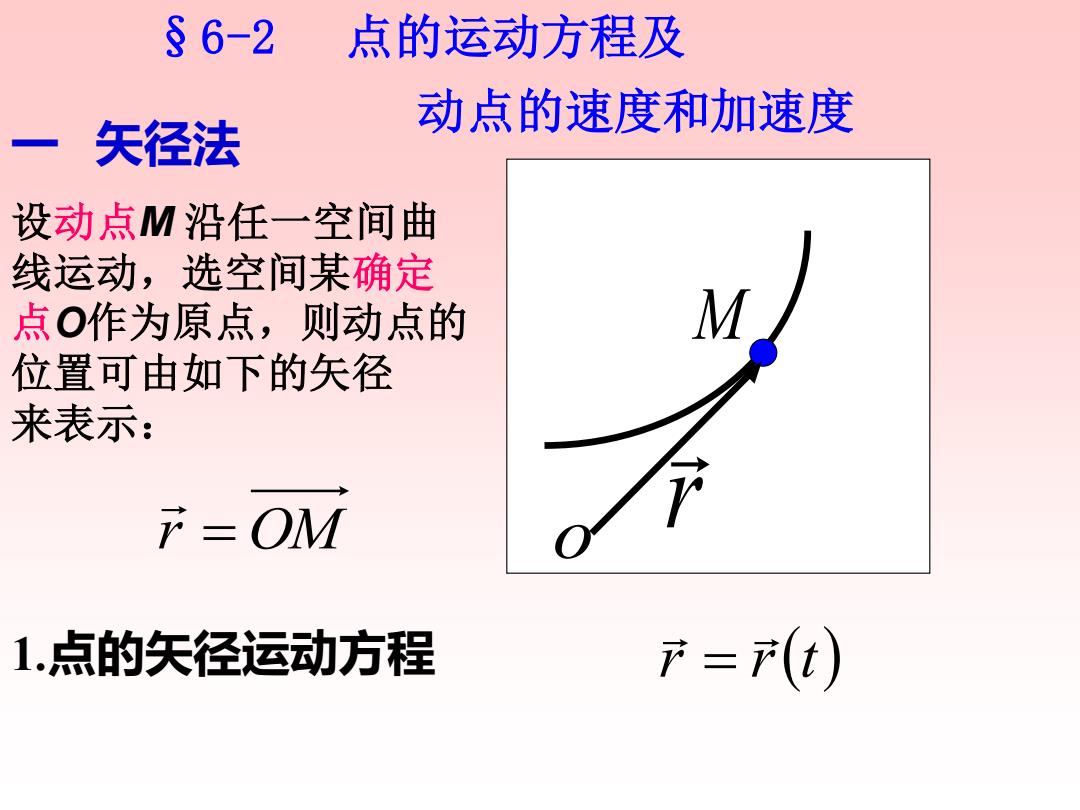
§6-2 点的运动方程及 动点的速度和加速度 一矢径法 设动点M沿任一空间曲 线运动,选空间某确定 点O作为原点,则动点的 位置可由如下的矢径 来表示: r OM 1.点的矢径运动方程 产=(t)
§6-2 点的运动方程及 动点的速度和加速度 一 矢径法 r = OM 1.点的矢径运动方程 r r(t) = 设动点M 沿任一空间曲 线运动,选空间某确定 点O作为原点,则动点的 位置可由如下的矢径 来表示: o M r
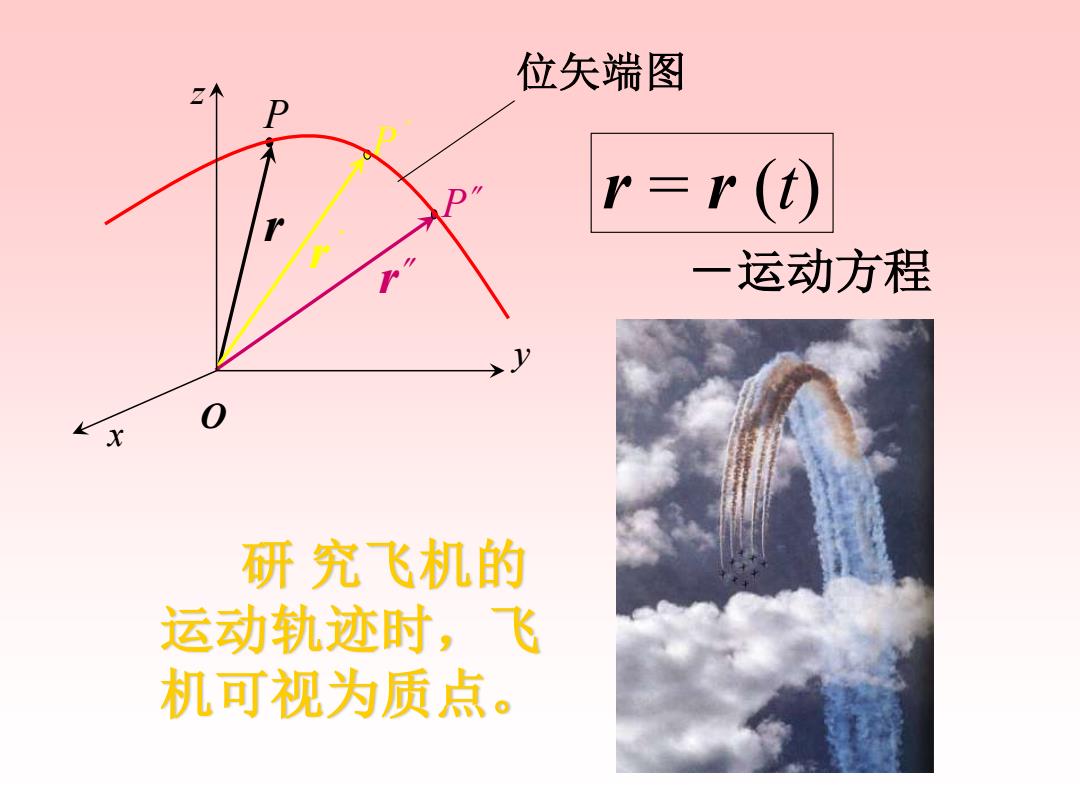
位矢端图 2个 r=r(t) 一运动方程 研究飞机的 运动轨迹时,飞 机可视为质点
r r ´ r r = r (t) P P´ P x z y O -运动方程 位矢端图 研 究飞机的 运动轨迹时,飞 机可视为质点