
第6章↓ 点的运动学 ★矢量法 ★ 直角坐标法 ★ 自然(弧坐标)法 ★ 应用举例
第6章 点的运动学 ★ 矢量法 ★ 直角坐标法 ★ 自然(弧坐标)法 ★ 应用举例

例 已知点的运动方程为xc=2sin4tm,y=2c0s4tm, z=4tm。 求:点的速度和加速度及运动轨迹的曲率半径p。 解:由点M的运动方程,得 v,==8cos4t,a,==-32sin 4t v==-8sin 4t,a,=j=-32cos4t y2=2=4,a=z=0 从而v=Vy:+2+v=v80m/小s,a=Va+a+a=32m/s2 而 dv a,= =0,an=a=32m/s2 dt 故 p= =2.5m An
例 已知点的运动方程为x=2sin 4t m,y=2cos 4t m, z=4t m。 求:点的速度和加速度及运动轨迹的曲率半径ρ。 解:由点M的运动方程,得 v x t a x t x = = 8cos 4 , x = = −32sin 4 v y t a y t y = = −8sin 4 , y = = −32cos 4 v = z = 4, a = z = 0 z z 2 2 2 2 2 2 2 = + + + = 80m s, = + + = 32m s x y z a ax ay az 从而 v v v v 2 m s d d = = 0, a = a = 32 t v 而 a n 2.5m 2 = = an v 故
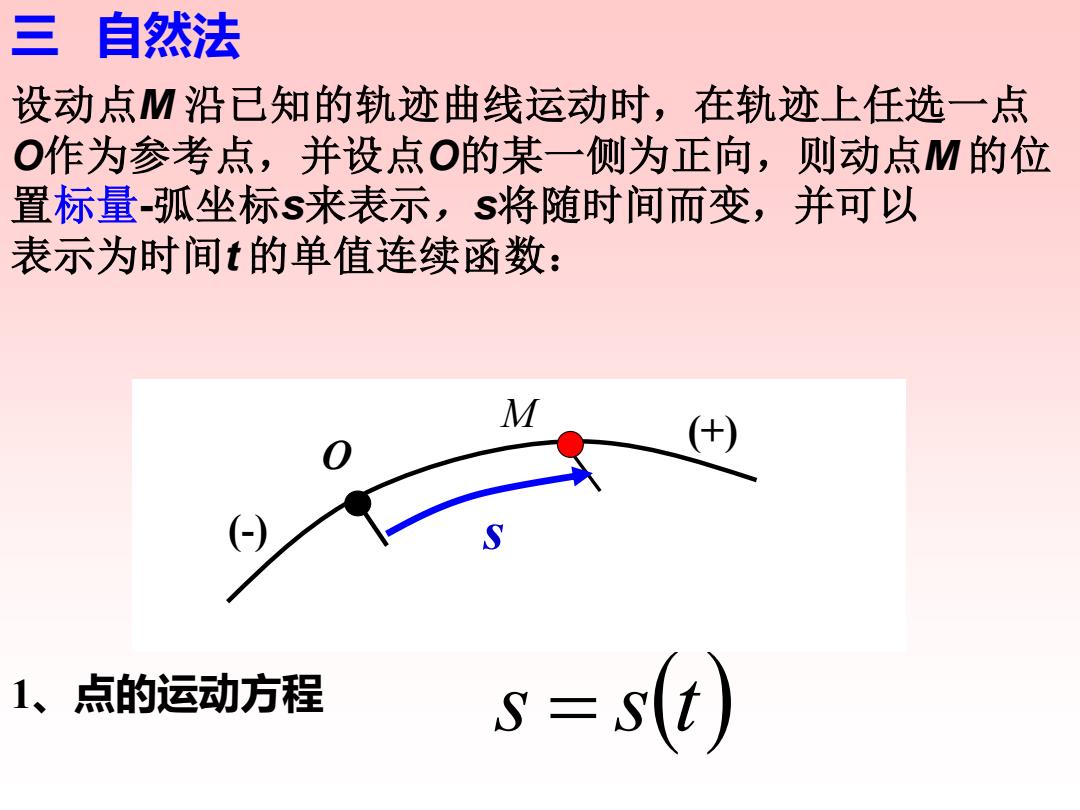
三自然法 设动点M沿已知的轨迹曲线运动时,在轨迹上任选一点 O作为参考点,并设点O的某一侧为正向,则动点M的位 置标量-弧坐标s来表示,s将随时间而变,并可以 表示为时间t的单值连续函数: M (牛) 1、点的运动方程 s=s(t)
三 自然法 设动点M 沿已知的轨迹曲线运动时,在轨迹上任选一点 O作为参考点,并设点O的某一侧为正向,则动点M 的位 置标量-弧坐标s来表示,s将随时间而变,并可以 表示为时间t 的单值连续函数: s = s(t) 1、点的运动方程 M s (+) (-) O
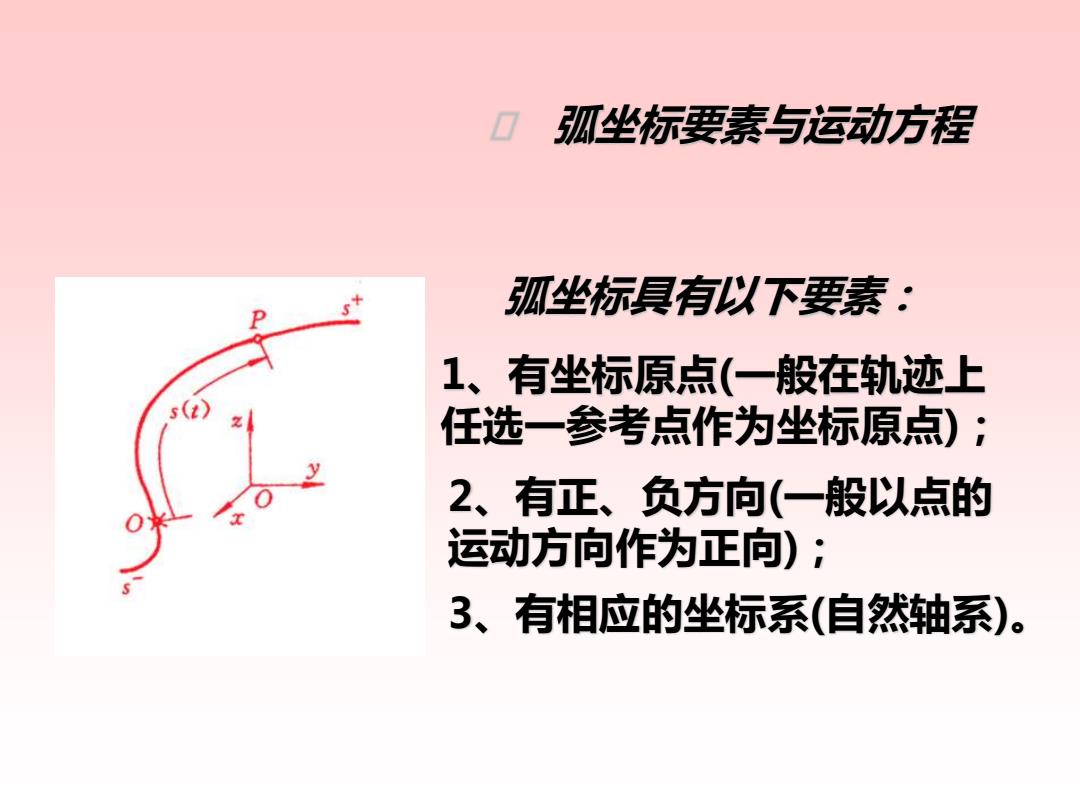
0 孤坐标要素与运动方程 孤坐标具有以下要素: 1、有坐标原点(一般在轨迹上 任选一参考点作为坐标原点): 2、有正、负方向(一般以点的 运动方向作为正向): 3、有相应的坐标系(自然轴系)
弧坐标要素与运动方程 弧坐标具有以下要素: 1、有坐标原点(一般在轨迹上 任选一参考点作为坐标原点); 2、有正、负方向(一般以点的 运动方向作为正向); 3、有相应的坐标系(自然轴系)
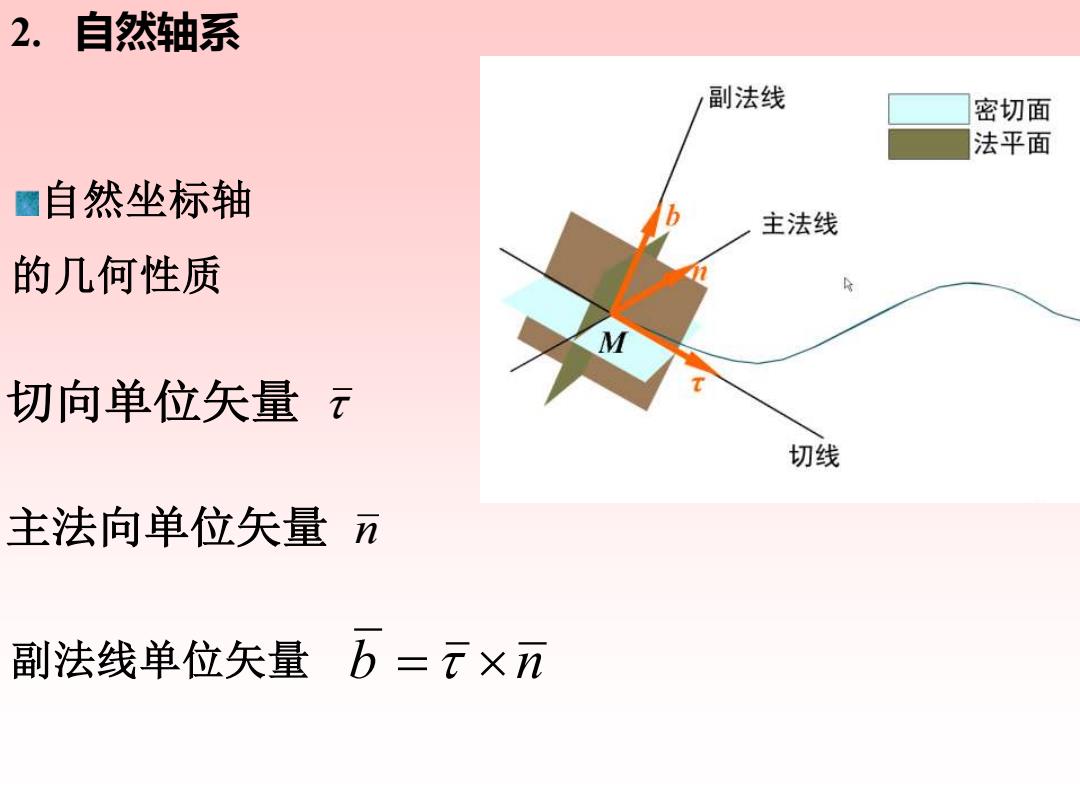
2.自然轴系 副法线 密切面 法平面 题自然坐标轴 主法线 的几何性质 令 切向单位矢量 切线 主法向单位矢量 副法线单位矢量b=元×n
自然坐标轴 的几何性质 副法线单位矢量 b = n 2. 自然轴系 主法向单位矢量 n 切向单位矢量