
第12章质点系动量矩定理 口动量矩 D 口动量矩定理 D 口刚体定轴转动微分方程 D 口质点系相对质心的动量矩定理 ☒ 口刚体平面运动微分方程 口讨论 周
第12章 质点系动量矩定理 □ 动量矩定理 □ 刚体定轴转动微分方程 □ 讨论 □质点系相对质心的动量矩定理 □ 刚体平面运动微分方程 □ 动量矩

§3.刚体定轴转动的微分方程 将质点系的动量矩定理 dHz=氵 Mz dt 及定轴转动的动量矩 H.=J0 应用于刚体定轴转动的情形,有: d(J2)=>M dt J,e=M2或J0=∑M 即为刚体定轴转动的微分方程。 与质心运动定理 Mac=∑F 比较之
§3. 刚体定轴转动的微分方程 将质点系的动量矩定理 z z dt d M H = 应用于刚体定轴转动的情形,有: 及定轴转动的动量矩 Hz = J z z z dt d( ) M J = z z z z J = M 或 J = M 即为刚体定轴转动的微分方程。 与质心运动定理 a = F 比较之。 M C
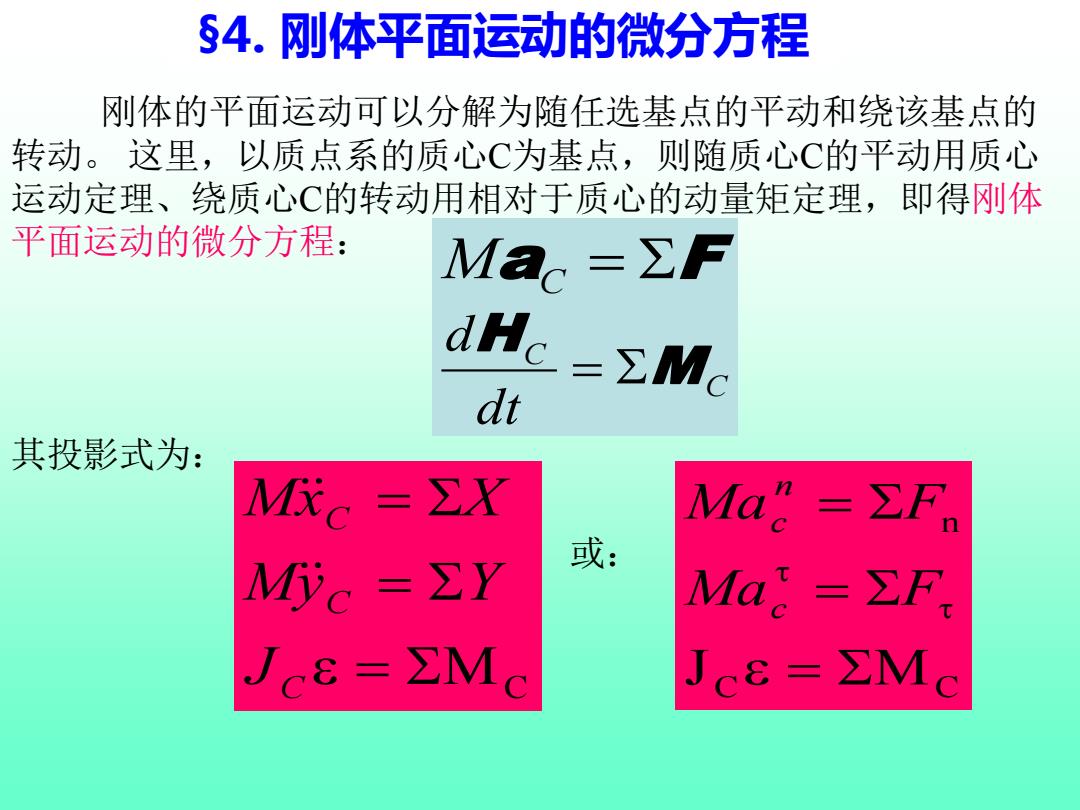
§4.刚体平面运动的微分方程 刚体的平面运动可以分解为随任选基点的平动和绕该基点的 转动。这里,以质点系的质心C为基点,则随质心C的平动用质心 运动定理、绕质心C的转动用相对于质心的动量矩定理,即得刚体 平面运动的微分方程: Mao=ΣF dHc=ZMc dt 其投影式为: M。=∑X Ma=∑F M。=∑Y 或: Mad=∑F, Jc&=∑MC Jc&=∑MC
§4. 刚体平面运动的微分方程 刚体的平面运动可以分解为随任选基点的平动和绕该基点的 转动。 这里,以质点系的质心C为基点,则随质心C的平动用质心 运动定理、绕质心C的转动用相对于质心的动量矩定理,即得刚体 平面运动的微分方程: = MC = = C C C J My Y Mx X C C n J = M = = Ma F Ma F c n c MaC = F C C dt d M H = 其投影式为: 或:
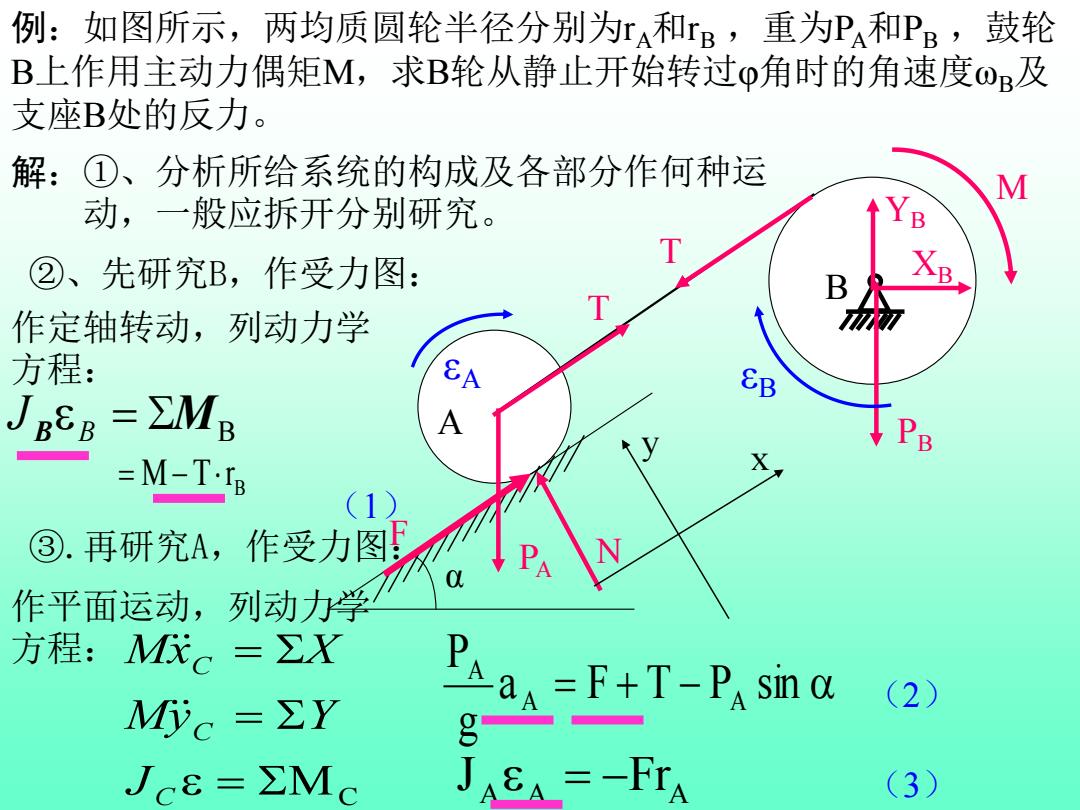
例:如图所示,两均质圆轮半径分别为ra和rB,重为P和PB,鼓轮 B上作用主动力偶矩M,求B轮从静止开始转过φ角时的角速度Q及 支座B处的反力。 解:①、分析所给系统的构成及各部分作何种运 M 动,一般应拆开分别研究。 ②、先研究B,作受力图: 作定轴转动,列动力学 方程: =∑MB A B =M-T-IB (1) ③.再研究A,作受力图 作平面运动,列动力学 方程:M代c=∑X Mc=∑Y Pa-F+T-P sin c (2) Jce=∑Mc --Fr (3)
例:如图所示,两均质圆轮半径分别为rA和rB ,重为PA和PB ,鼓轮 B上作用主动力偶矩M,求B轮从静止开始转过φ角时的角速度ωB及 支座B处的反力。 α B A M PA PB 解:①、分析所给系统的构成及各部分作何种运 动,一般应拆开分别研究。 ②、先研究B,作受力图: YB XB T 作定轴转动,列动力学 方程: B = MB B J B = M −Tr (1) εB ③.再研究A,作受力图: N T F εA 作平面运动,列动力学 方程: = MC = = C C C J My Y Mx X a = F + T − P sin g P A A A A A FrA J = − (2) (3) x y

再列补充方程一一般为运动学关系: TAEA -aA (4) TAEA TBEB (5) 以上5个未知量均可求解。从中解出为常量,则有: @o+28p M 欲求支座反力,则需对轮B列质心运动定理T M优c=∑X PE0=Xn-Tcosa. (6) 8 Mc=ΣY BA0=卫2P。-Tsm0 (7) X
再列补充方程—— 一般为运动学关系: A A A r = a A A B B r = r (4) (5) 以上5个未知量均可求解。从中解出εB为常量,则有: = + B 2 0 2 B 2 欲求支座反力,则需对轮B列质心运动定理: My Y Mx X C C = = = − − = − P Tsin Tcos B B B B B 0 Y g P 0 X g P (6) (7) B M PB YB XB T x y