
第4章 空间力系的简化和平衡 §4-3空间力偶理论 §4-4空间任意力系的简化和平衡 §4-5平行力系中心与重心
第4章 空间力系的简化和平衡 §4-3 空间力偶理论 §4-4 空间任意力系的简化和平衡 §4-5 平行力系中心与重心
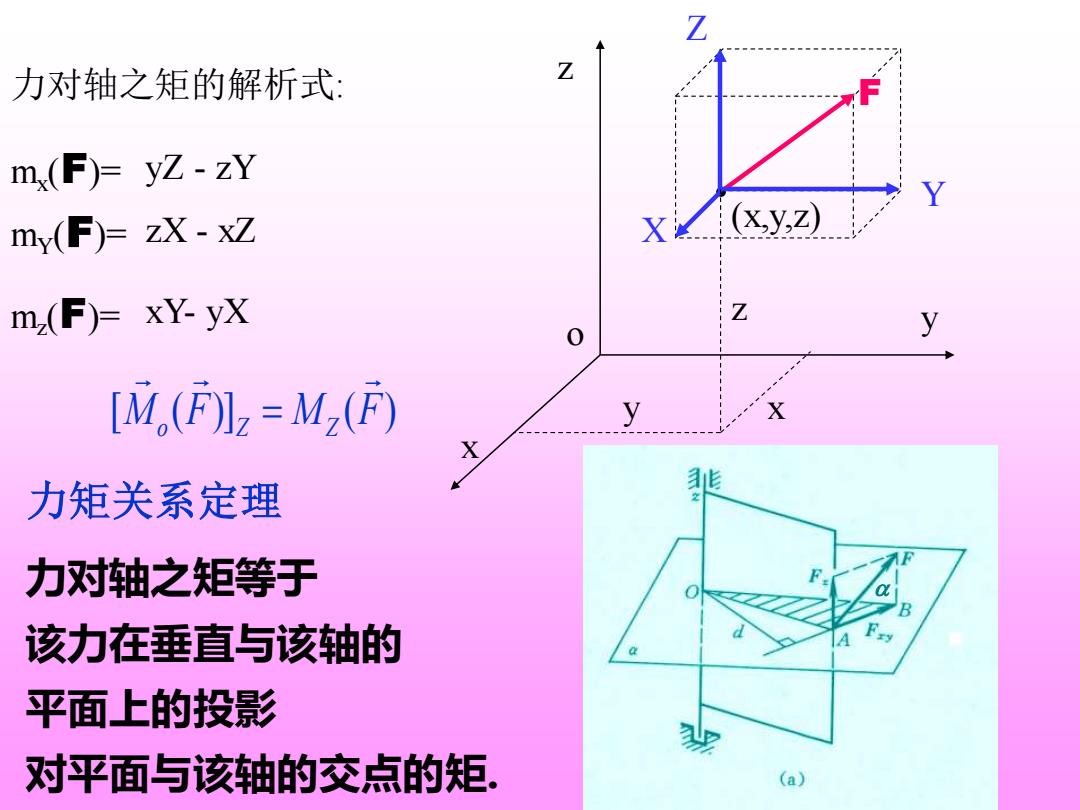
Z 力对轴之矩的解析式: Z m(F)=yZ-zY my(F)=zX-xZ X (x,y,z) m(F)=xY-yX Z 0 y [M,(F]2=M,(F) y X X 力矩关系定理 力对轴之矩等于 该力在垂直与该轴的 平面上的投影 对平面与该轴的交点的矩。 (a)
z y x o 力对轴之矩的解析式: (x,y,z) . F X Y Z z y x mx (F)= yZ - zY mY(F)= zX - xZ mz (F)= xY- yX [M (F)] M (F) o Z Z = 力对轴之矩等于 该力在垂直与该轴的 平面上的投影 对平面与该轴的交点的矩. 力矩关系定理

§4-3 空间力偶理论 一.空间力偶的性质 作用于同一物体上的 大小相等,方向相反 且不共线的两个力 组成的特殊力系
一. 空间力偶的性质 §4-3 空间力偶理论 作用于同一物体上的 大小相等,方向相反 且不共线的两个力 组成的特殊力系
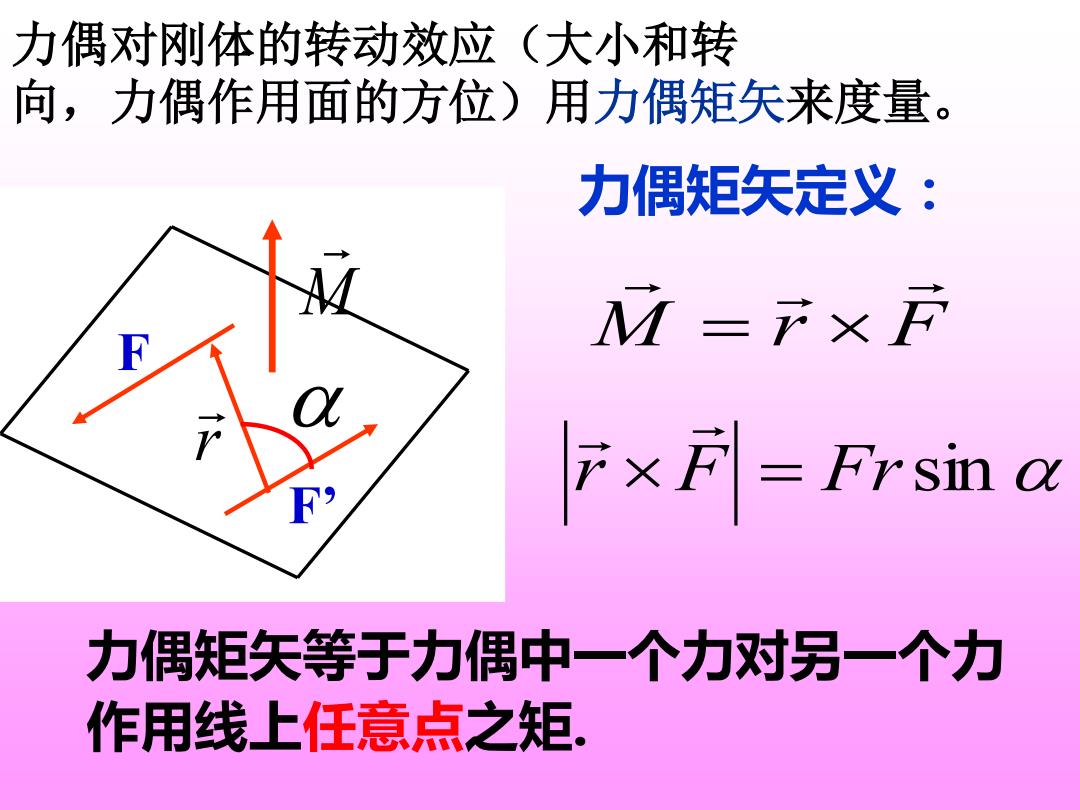
力偶对刚体的转动效应(大小和转 向,力偶作用面的方位)用力偶矩矢来度量。 力偶矩矢定义: M= F× ×F=Frsin a 力偶矩矢等于力偶中一个力对另一个力 作用线上任意点之矩
力偶对刚体的转动效应(大小和转 向,力偶作用面的方位)用力偶矩矢来度量。 力偶矩矢定义: M r F = r F = Frsin F F’ M r 力偶矩矢等于力偶中一个力对另一个力 作用线上任意点之矩
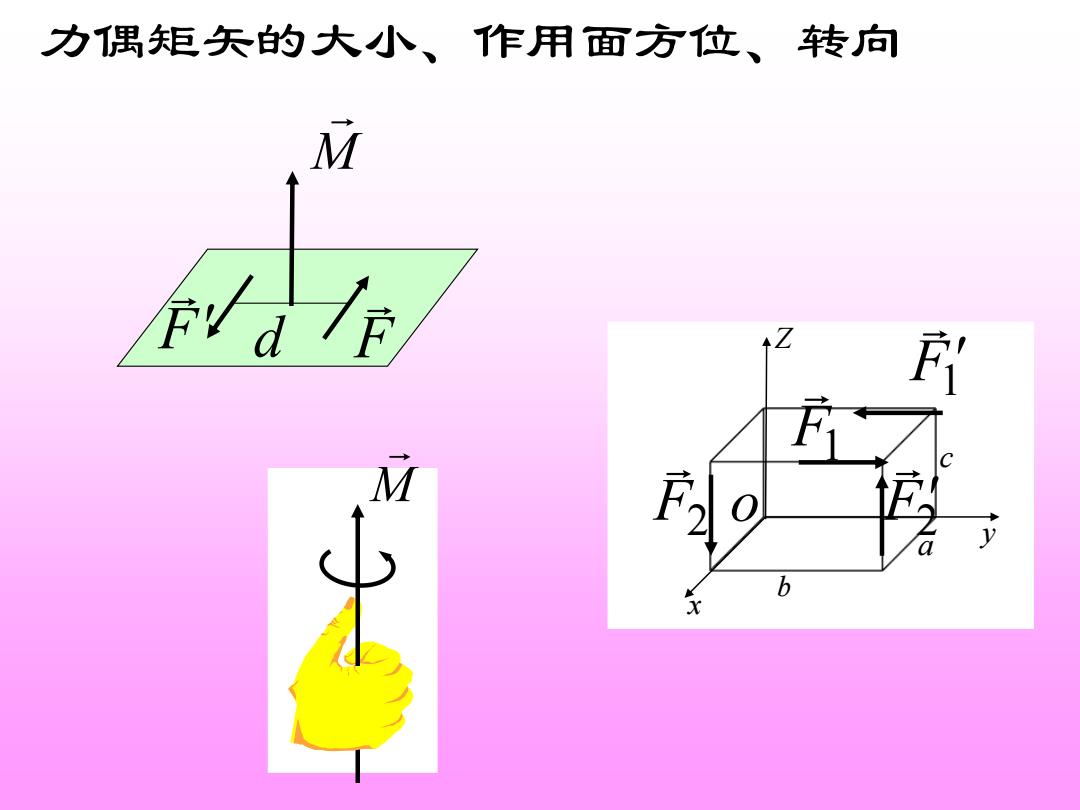
力偶矩矢的大小、作用面方位、转向 m M b
x y o Z a b 1 c F F1 F2 F2 M 力偶矩矢的大小、作用面方位、转向 F F d M