
第13章i 动静法(达朗贝尔原理) §13-1 惯性力,质点的达朗贝尔原理 §13-2 质点系的达朗贝尔原理 §13-3 定轴转动刚体的轴承动反力
第13章 动静法(达朗贝尔原理) §13-1 惯性力,质点的达朗贝尔原理 §13-2 质点系的达朗贝尔原理 §13-3 定轴转动刚体的轴承动反力

达朗伯原理(动静法) 达朗伯原理(动静法)是将动力学问题在形式上 转化成静力学平衡问题并求解的一种方法。 达朗伯原理是解决非自由质点系动力学的一种 普遍方法。对于已知运动(x、v、a)求约束反力 的工程问题特别方便
达朗伯原理(动静法) 达朗伯原理是解决非自由质点系动力学的一种 普遍方法。对于已知运动(x、v、a)求约束反力 的工程问题特别方便。 达朗伯原理(动静法)是将动力学问题在形式上 转化成静力学平衡问题并求解的一种方法
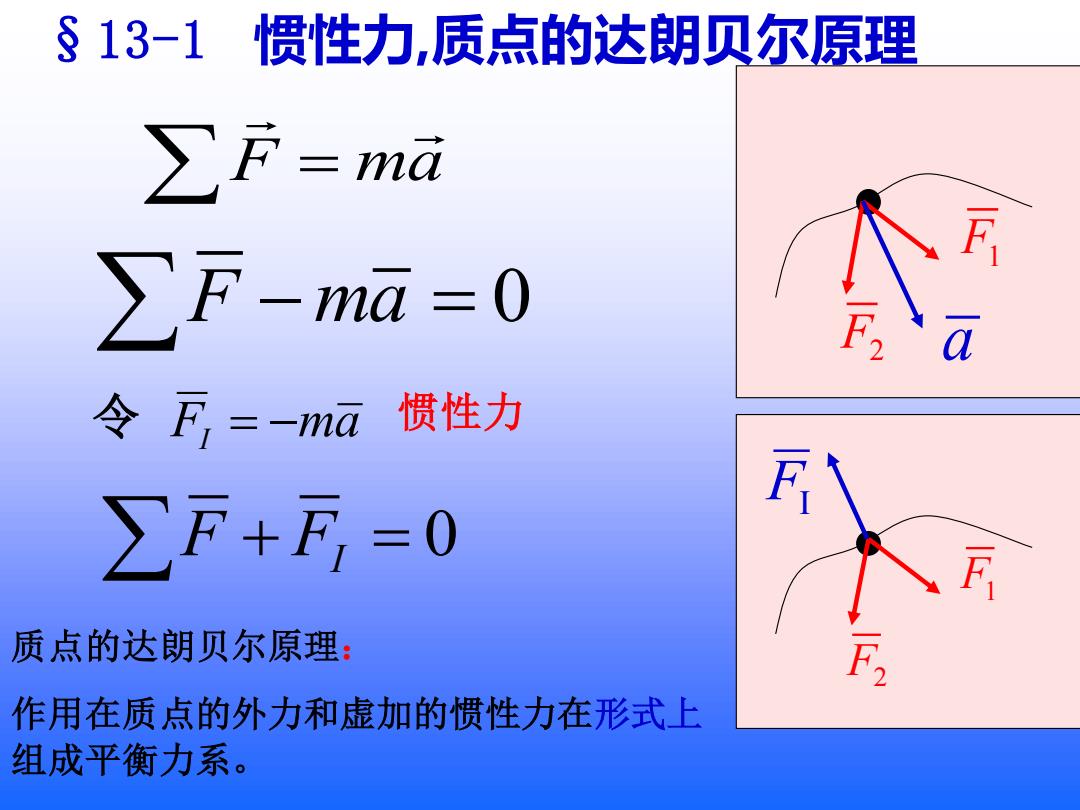
§13-1 惯性力,质点的达朗贝尔原理 ∑F=md F ∑F-ma=0 a 令F=-ma 惯性力 ∑F+F,=0 F 质点的达朗贝尔原理: 作用在质点的外力和虚加的惯性力在形式上 组成平衡力系
§13-1 惯性力,质点的达朗贝尔原理 F −ma = 0 令 FI = −ma 惯性力 F + FI = 0 质点的达朗贝尔原理: 作用在质点的外力和虚加的惯性力在形式上 组成平衡力系。F ma = F1 F2 a F1 F2 FI
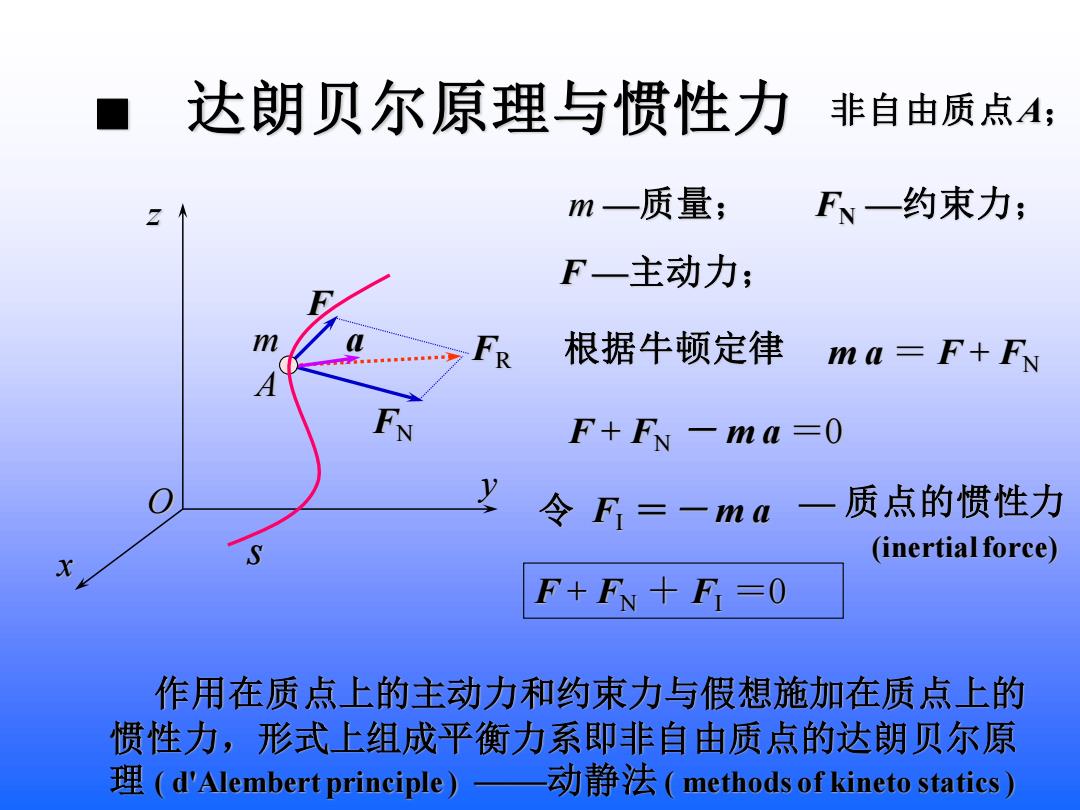
达朗贝尔原理与惯性力 非自由质点A; m一质量; F一约束力; F一主动力; FR 根据牛顿定律 ma=F+F F+F-ma=0 令F=-ma- 质点的惯性力 (inertial force) F+FN+F-0 作用在质点上的主动力和约束力与假想施加在质点上的 惯性力,形式上组成平衡力系即非自由质点的达朗贝尔原 理(d'Alembert principle)—动静法(methods of kineto statics)
FN FR F a x z y O m A 非自由质点A; m —质量; s FN —约束力; F —主动力; ■ 达朗贝尔原理与惯性力 根据牛顿定律 m a = F + FN F + FN - m a =0 令 FI =- m a F + FN + FI =0 作用在质点上的主动力和约束力与假想施加在质点上的 惯性力,形式上组成平衡力系即非自由质点的达朗贝尔原 理 ( d'Alembert principle ) ——动静法 ( methods of kineto statics ) — 质点的惯性力 (inertial force)

∑F+F,=0 即:∑F=0 该方程对动力学问题来说只是形式上的平衡, 并没有改变动力学问题的实质。采用动静法解决 动力学问题的最大优点,可以利用静力学提供的 解题方法,给动力学问题一种统一的解题格式
该方程对动力学问题来说只是形式上的平衡, 并没有改变动力学问题的实质。采用动静法解决 动力学问题的最大优点,可以利用静力学提供的 解题方法,给动力学问题一种统一的解题格式。 即: F = 0 F + FI = 0