
P(X=m)2P(X=m-1),得 2-m≥0 P(X=m)≥P(X=m+1)m+1-≥0 故2-1≤m≤2. 综上所述,当2为正整数时,P(X=兄)=P(X=2-1) 为最大;而当2不是正整数时,当m=I2/时,P(X=m) 取得最大值。 冈✉圆
m . , m m , P( X m ) P( X m ) P( X m ) P( X m ) − + − − = = + = = − 1 1 0 0 1 1 故 得 取得最大值。 为最大;而当 不是正整数时,当 时 , 综上所述,当 为正整数时, m [ ] P( X m ) P( X ) P( X ) = = = = = − 1
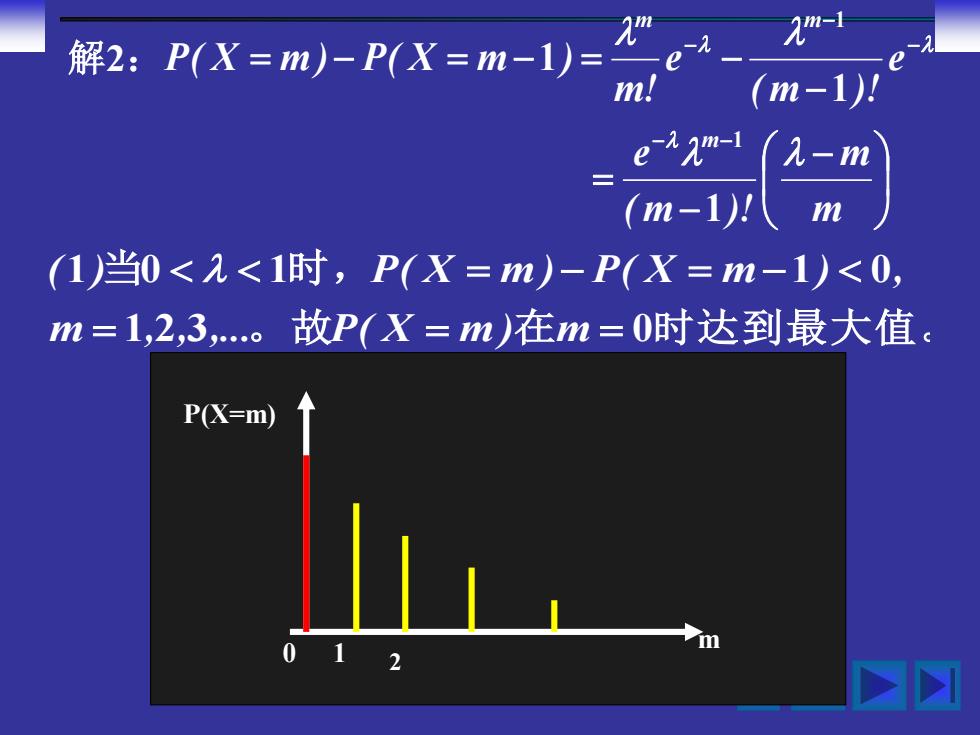
e> 2m-1 解2:P(X=m)-P(X=m-1)= m! (m-1)1 (1)当0<2<1时,P(X=m)-P(X=m-1)<0, m=1,2,3,。故P(X=m)在m=0时达到最大值. P(X=m)
解2: − − = − = − = − = − − − − − − m m ( m )! e e ( m )! e m! P( X m ) P( X m ) m m m 1 1 1 1 1 。 故 在 时达到最大值。 当 时 , 1 2 3 0 1 0 1 1 0 = = = = − = − m , , ,. P( X m ) m ( ) P( X m ) P( X m ) , P(X=m) m 0 1 2
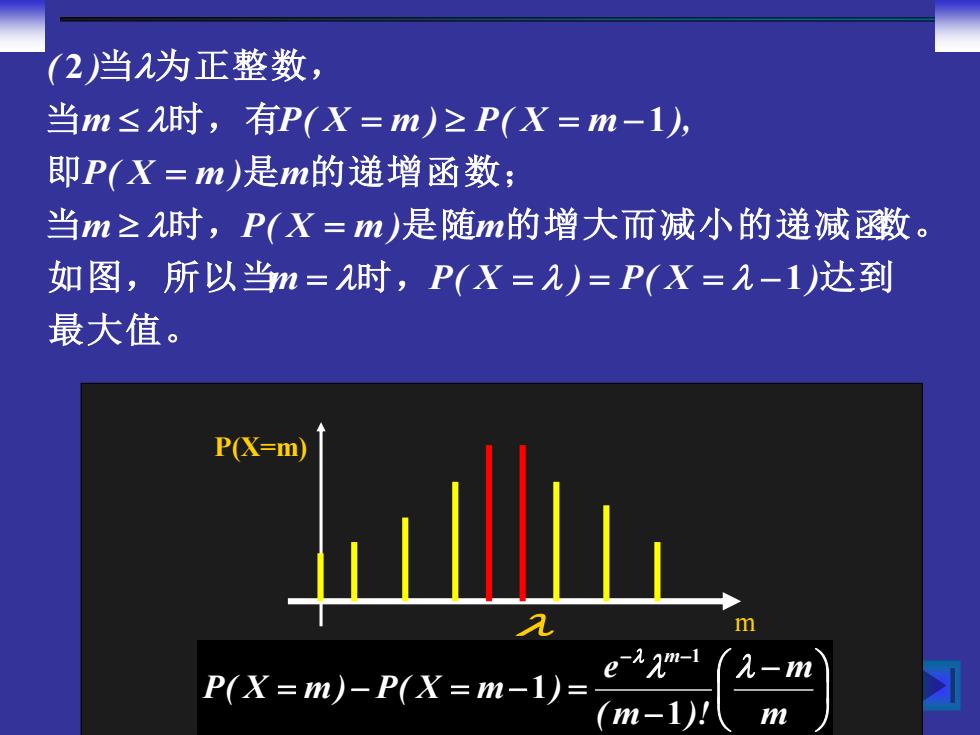
(2当为正整数, 当m≤时,有P(X=m)≥P(X=m-1, 即P(X=m)是m的递增函数; 当m≥时,P(X=m)是随m的增大而减小的递减函数。 如图,所以当m=时,P(X=2)=P(X=-1达到 最大值。 P(X=m) m P(X=m)-P(X=m-1)= e22mw-1(-m (m-1)八
最大值。 如图,所以当 时 , 达 到 当 时 , 是 随 的增大而减小的递减函数 。 即 是 的递增函数; 当 时,有 当 为正整数, m P( X ) P( X ) m P( X m ) m P( X m ) m m P( X m ) P( X m ), ( ) 1 1 2 = = = = − = = = = − P(X=m) m − − = − = − = − − m m (m )! e P( X m ) P( X m ) m 1 1 1

3) 若入不是正整数, 当m≤I2/时(m<元<m+1),有P(X=m)>P(X=m-1)月 即P(X=m)是m的严格递增函数; 当m≥I2/时,有P(X=m)<P(X=m-1)即P(X=m》 是m的严格递减函数。如图所以当m=I2/时,P(X=m) 取得最大值。 P(X=m) []
[] m P(X=m) 取得最大值。 是 的严格递减函数。如图,所以当 时 , 当 时,有 , 即 即 是 的严格递增函数; 当 时 有 () 若 不是正整数, m m [ ] P( X m ) m [ ] P( X m ) P( X m ) P( X m ) P( X m ) m m [ ] ( m m ), P( X m ) P( X m ), = = = = − = = + = = − 1 1 1 3

综上所述,当2为正整数时,P(X=2)=P(X=入-1) 为最大;而当2不是正整数时,当m=/2/时,P(X=m) 取得最大值。 冈✉圆
取得最大值。 为最大;而当 不是正整数时,当 时 , 综上所述,当 为正整数时, m [ ] P( X m ) P( X ) P( X ) = = = = = − 1