
函数在某点各偏导数都存在,但在该点不一定连续xy例如,z= f(x,y) =Cd显然fx(0, 0)=f(x, 0)x=0=0dxdf,(0, 0) =f(0, y)V=0=0dy在上节已证f(x,J)在点(0,0)并不连续!0000专方下页返回洁乐
函数在某点各偏导数都存在, 显然 例如, + = + = = + 0 , 0 , 0 ( , ) 2 2 2 2 2 2 x y x y x y xy z f x y = 0 = 0 但在该点不一定连续. 上节例 目录 上页 下页 返回 结束 在上节已证 f (x , y) 在点(0 , 0)并不连续!

例1.求z=x2+3xy+2在点(1,2)处的偏导数Ozaz解法1:3x +2yaxayOzOzy/(,2)=3.1+ 2.2 = 7=2·1+3.2=8.0x(1,2)解法2:y=2= x2 +6x+ 4az0x/(1, 2) =(2x + 6)=8X=[x=1 =1+3y+ y2azy(1, 2)= (3+ 2y)2=1一目录下页反回结束
例1 . 求 2 2 z = x + 3xy + y 解法1: = x z x (1,2) z 解法2: x (1, 2) z 在点(1 , 2) 处的偏导数. y (1, 2) z 2x + 3y , = y z 3x + 2y y (1,2) z 6 4 2 = x + x + x=1 z 2 =1+ 3y + y y=2 z 机动 目录 上页 下页 返回 结束

常数和基本初等函数的导数(x")= uxu-I(C)= 0(a")= a"lna(e")= er(lnx)= 1(log. x) =xlnaX(sinx)= cosx(cosx)'= -sinx(cot x)' = -csc’ x(tanx)'= sec2 x(csc x)'= -cscxcot x(secx)= secx tanx(arccos x)':(arcsin x)' =V/1- xV1-(arctan x)' =(arc cot x)"1+x1+x
常数和基本初等函数的导数 ( )x a = ln x a a ( )x e = x e (log ) a x = 1 x a ln (ln ) x = 1 x (arcsin ) x = 2 1 1− x (arccos ) x = 2 1 1 x − − (arctan ) x = 2 1 1+ x (arccot ) x = 2 1 1 x − + (sin ) x = cos x (cos ) x = −sin x (tan ) x = 2 sec x (cot ) x = 2 −csc x (sec ) x = sec tan x x (csc ) x = ( ) C = 0 ( ) x = 1 x − −csc cot x x
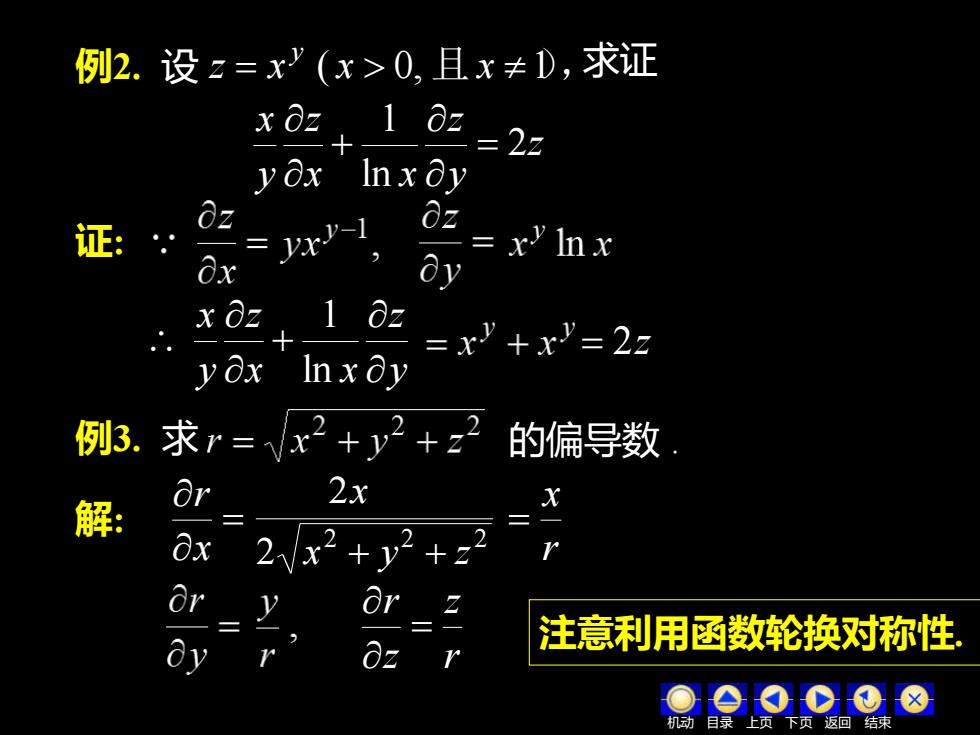
例2.设z=x(x>0,且x±D,求证x Oz1 Oz:2z一yoxIn x OyOzOzvry-证:xln xayaz07-xs=22XyoxIn x Oy例3.求r=的偏导数x~+yOr2Xx解:OxOrd注意利用函数轮换对称性az十目录-下页反回结束
例2. 设 z = x y ( x 0, 且 x 1), z y z x x z y x 2 ln 1 = + 证: y z x x z y x + ln 1 例3. 求 的偏导数 . 解: = x r 求证 = 2z 2 2 2 2 x + y + z 2x r x = r z z r = 机动 目录 上页 下页 返回 结束 注意利用函数轮换对称性