
商集即划分 假设R是集合A上的等价关系,给定aEA,R(a)是 由R所诱导的等价类。 Q={R(|x∈A}是相应的商集。 口容易证明,这样的商集即是A的一个划分: 口对任意a∈A,a∈R(a)(R是自反的) 口对任意a,b∈A,(a,bR当且仅当R(a∩R(b)=☑,即: 不相等的等价类必然不相交
商集即划分 假设R是集合A上的等价关系,给定aA, R(a)是 由R 所诱导的等价类。 Q={R(x)|xA}是相应的商集。 容易证明,这样的商集即是A的一个划分: 对任意 aA, aR(a) (R 是自反的) 对任意 a,bA, (a,b) R 当且仅当 R(a)R(b)= ,即: 不相等的等价类必然不相交

商集即划分 不相等的等价类必然不相交。换句话说,有公共元 素的任意两个等价类必然相等。 证明: ▣假设R(a)⌒R(b≠O,设c是一个公共元素。 口根据等价类的定义,(a,G∈R,(b,c∈R 口对任意x∈R(a,(a,)∈R,由R的传递性和对称性,可得 (c,∈R,由此可知(b,∈R即x∈R(⑤),.R(aCR(b) 口同理可得:R(b)cR(a)。因此:R(a)=R(b)
不相等的等价类必然不相交。换句话说,有公共元 素的任意两个等价类必然相等。 证明: 假设R(a)R(b)Ø, 设c是一个公共元素。 根据等价类的定义,(a,c)R, (b,c)R 对任意xR(a), (a,x)R, 由R的传递性和对称性,可得 (c,x)R, 由此可知(b,x)R, 即xR(b), R(a)R(b) 同理可得:R(b)R(a)。因此: R(a)=R(b) 商集即划分
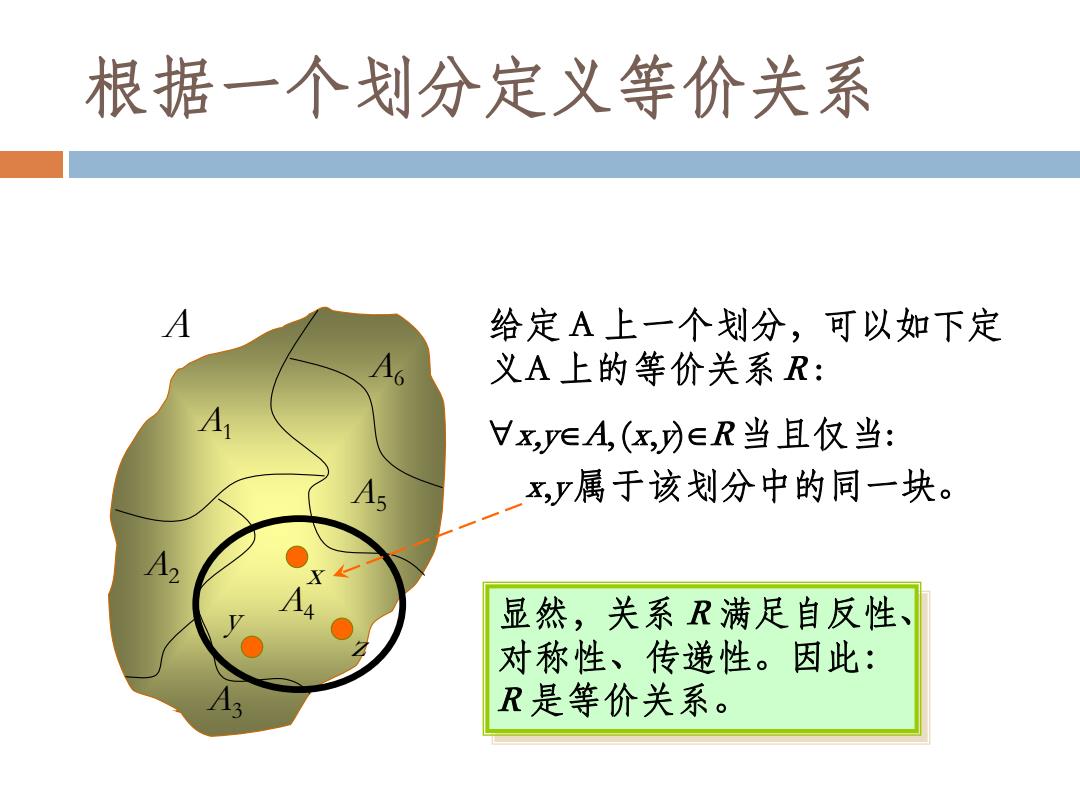
根据一个划分定义等价关系 A 给定A上一个划分,可以如下定 As 义A上的等价关系R: A VXVEA,(☒の∈R当且仅当: As x,y属于该划分中的同一块。 A 显然,关系R满足自反性、 对称性、传递性。因此: R是等价关系
A1 A6 A5 A4 A3 A2 A x y z 给定 A 上一个划分,可以如下定 义A 上的等价关系R : x,yA, (x,y)R 当且仅当: x,y属于该划分中的同一块。 显然,关系 R 满足自反性、 对称性、传递性。因此: R 是等价关系。 根据一个划分定义等价关系

利用等价类解题 口证明: 从1,2,,2000中任取1001个数,其中必有两个 数x,y,满足x/y=2。 (k为整数)。 想起鸽笼原理没?
证明: 从1,2,...,2000中任取1001个数,其中必有两个 数x,y,满足x/y=2 k 。 (k为整数)。 想起鸽笼原理没? 利用等价类解题

利用等价类解题 建立1000个集合,每个集合包括1至2000之间的一个奇数以 及该奇数与2的k次幂的乘积,但最大不超过2000。可以证 明这1000个集合的集合是集合{1,2,3,,2000}上的一个划分。 注意任意两个1到2000之间的正整数x,y在同一划分块中当 且仅当x/y=2。(k为整数)。 ▣定义集合{12,3,2000}上的一个关系R,任意xy,xy当且仅当 x/y=2。易证这是一个等价关系。其商集即集合上面的划分
建立1000个集合, 每个集合包括1至2000之间的一个奇数以 及该奇数与2的k次幂的乘积, 但最大不超过2000。可以证 明这1000个集合的集合是集合{1,2,3,..., 2000}上的一个划分。 注意任意两个1到2000之间的正整数x,y在同一划分块中当 且仅当x/y=2 k 。(k为整数)。 定义集合{1,2,3,..., 2000}上的一个关系R,任意x,y,xRy当且仅当 x/y=2 k 。易证这是一个等价关系。其商集即集合上面的划分。 利用等价类解题