
等价类的代表元素 对于等价类[国{y|EAAXRY},x称为这个等 价类的代表元素 口其实,该等价类的每个元素都可以做代表元素: 若xRy,则[图=[ 口证明:对任意元素若t[☒,则xR:根据R的对称性与传 递性,且xRy可得R:因此t[☑,[国小;同理可得 [c[☒
等价类的代表元素 对于等价类[x]R={ y | yA xRy },x称为这个等 价类的代表元素. 其实,该等价类的每个元素都可以做代表元素: 若xRy,则[x]=[y] 证明:对任意元素t, 若t[x], 则xRt, 根据R的对称性与传 递性,且xRy, 可得yRt, 因此 t[y], [x][y]; 同理可得 [y][x]

例 口R,R2分别是集合X,上的等价关系。定义X×上的关系S: (☒12)S(U1,)当且仅当x1R11且x2R22 0 证明:S是X×上的等价关系 口[自反性]对任意(区の∈X1×X2,由R1,R2满足自反性可知,(☒,)∈R1, (の∈R2;∴.(x)Sx防S自反。 口[对称性]假设(1,)S(2),由S的定义以及R1,R2满足对称性可 知:(12)S(1,;S对称。 口[传递性]假设(☒1)S(1,),且(1,)S(1,),则x1R1,1R1么, 2R22,2R22,由R1,R2满足传递性可知:1R1,且R22,于是: (x1,x)S(21,22;S传递
例 R1 ,R2分别是集合X1 ,X2上的等价关系。定义X1X2上的关系S: (x 1 ,x 2 )S (y 1 ,y2 ) 当且仅当x 1R1 y 1且 x 2R2 y 2 证明:S是X1X2上的等价关系 [自反性] 对任意(x,y)X1X2 , 由R1 ,R2满足自反性可知, (x,x)R1 , ( y,y) R2 ; (x,y)S(x,y); S自反。 [对称性] 假设( x 1 ,x2 )S ( y 1 ,y 2 ), 由S的定义以及R1 ,R2满足对称性可 知: ( y 1 ,y 2 )S (x 1 ,x2 ); S对称。 [传递性] 假设(x 1 ,x 2 )S ( y 1 ,y2 ), 且( y 1 ,y2 )S ( z 1 ,z 2 ), 则x 1R1y 1 , y 1R1z1 , x 2R2y2 , y 2R2z 2 , 由R1 ,R2满足传递性可知:x 1R1z1 , 且x 2R2z2 , 于是: (x 1 ,x2 )S (z 1 ,z 2 ); S传递

商集 R是非空集合A上的等价关系,x∈A,则其所有等价 类的集合称为商集,记为A/R 口例子 口集合A={a1,2,…,a}上的恒等关系是等价关系,商集 A/Ia={a1},{a2},…,{an} 口整数集上的模3同余关系是等价关系,其商集为{{…, -6,-3,0,3,6,9,…},{…,-5,-2,1,4,7,…},{…,-4,-1,2, 5,8,11,…}}
商集 R是非空集合A上的等价关系,xA,则其所有等价 类的集合称为商集,记为A/R 例子 集合A={a 1 ,a 2 , …, a n}上的恒等关系IA是等价关系,商集 A/IA={{a1}, {a 2},…, {a n}} 整数集上的模3同余关系是等价关系,其商集为{ {…, -6, -3, 0, 3, 6, 9, …}, {…, -5, -2, 1, 4, 7, …}, {…, -4, -1, 2, 5, 8, 11, …} }

例 口定义自然数集的笛卡儿乘积上的关系R (a,b)R(c,d当且仅当a+d=b+c 证明这是等价关系,并给出其商集. 口定义在N上的二元关系R:xRy iff x=2ky(k为 整数) (1)试证明R是等价关系; (2)给出商集N/R,并证明N与N/R等势
例 定义自然数集的笛卡儿乘积上的关系R: (a, b)R(c,d) 当且仅当 a+d=b+c 证明这是等价关系,并给出其商集. 定义在ℕ上的二元关系𝑅: x𝑅y iff 𝑥 = 2 𝑘𝑦 (k为 整数). (1)试证明𝑅是等价关系; (2)给出商集ℕ/𝑅,并证明ℕ与ℕ/𝑅等势
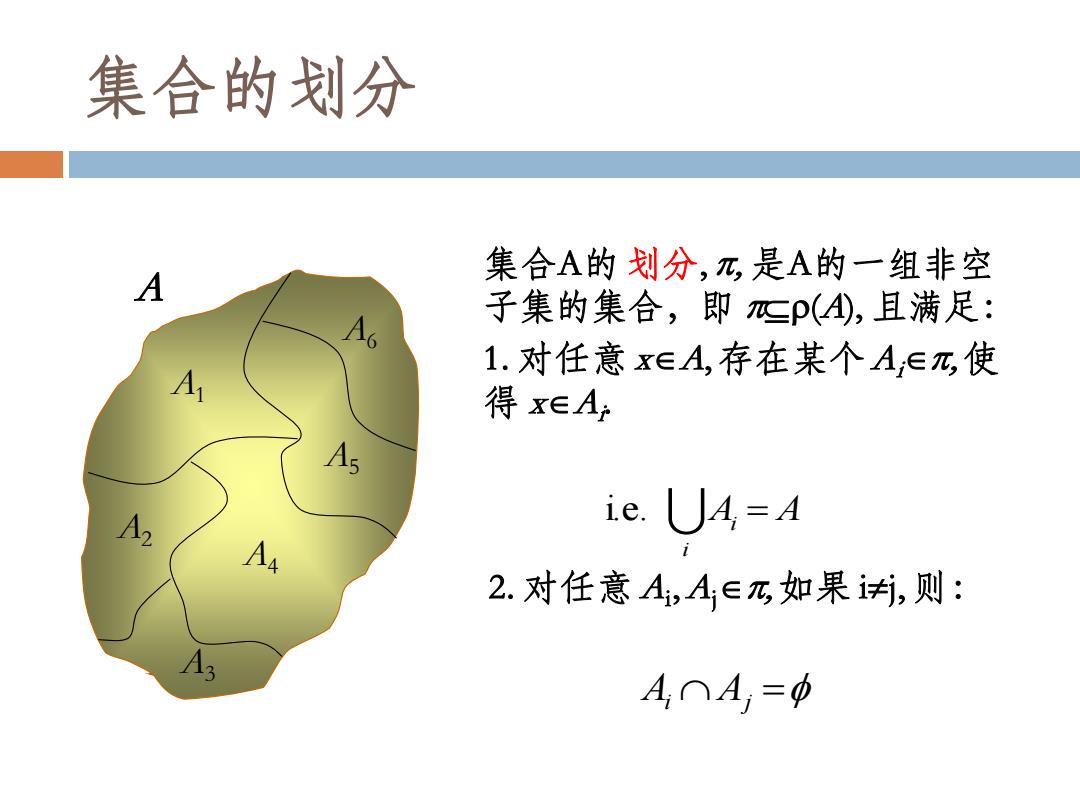
集合的划分 集合A的划分,元,是A的一组非空 A 子集的集合,即p(,且满足: A 1.对任意x∈A,存在某个A∈兀,使 得x∈A: As ie.4=4 2.对任意A,A∈乃,如果j,则: A3 A,∩A,=中
A1 A6 A5 A4 A3 A2 A 集合A的划分, , 是A的一组非空 子集的集合,即 (A), 且满足: 1. 对任意 xA, 存在某个Ai, 使 得 xAi . A A i i.e. i = 2. 对任意 Ai ,Aj,如果 ij, 则: Ai Aj = 集合的划分