
FIR滤波器基本网络结构 本书将讨论下面四种结构: 直接形式:以直接实现差分方程而得名。 级联形式:它把多项式H(z)分解成多个二阶因式, 然后用级联连接。 线性相位形式:当FR滤波器具有线性相位响应 时,根据5.5节,它的脉冲响应具有对称性。因 此能把倍率的计算量缩至一半。 频率采样形式:这种结构基于脉冲响应h(n)的 DFT,,其结果可以形成一个并联结构。 21
21 FIR滤波器基本网络结构 本书将讨论下面四种结构: 直接形式:以直接实现差分方程而得名。 级联形式:它把多项式H(z)分解成多个二阶因式, 然后用级联连接。 线性相位形式:当FIR滤波器具有线性相位响应 时,根据5.5节,它的脉冲响应具有对称性。因 此能把倍率的计算量缩至一半。 频率采样形式:这种结构基于脉冲响应h(n)的 DFT,,其结果可以形成一个并联结构
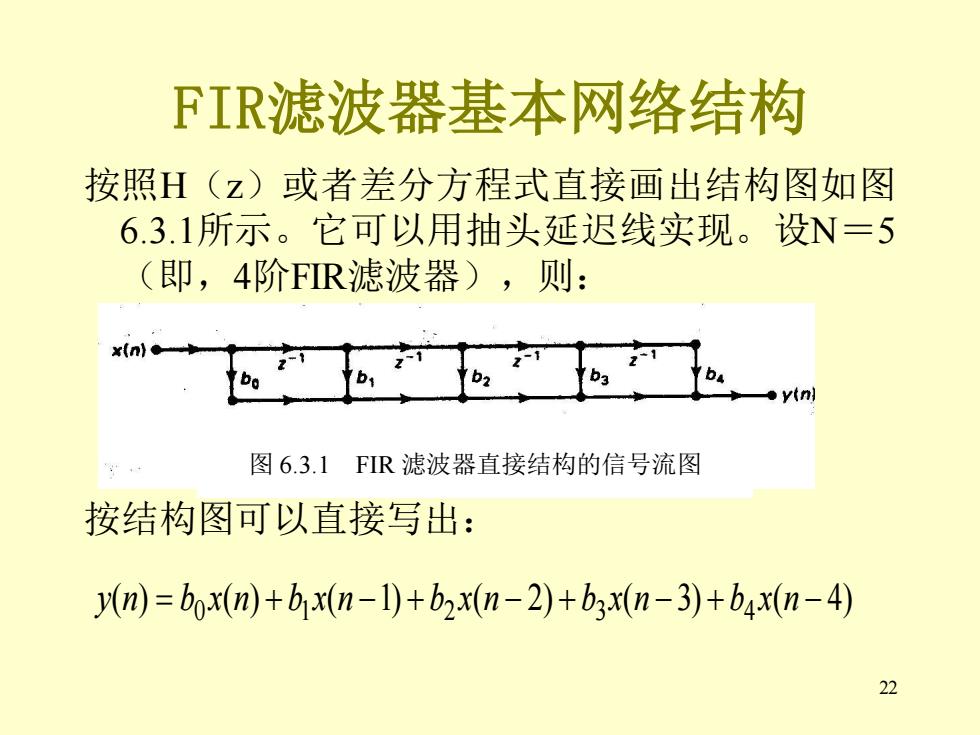
FIR滤波器基本网络结构 按照H(z)或者差分方程式直接画出结构图如图 6.3.1所示。它可以用抽头延迟线实现。设N=5 (即,4阶FR滤波器),则: xnl● 图63.1FIR滤波器直接结构的信号流图 按结构图可以直接写出: y(n)=box(n)+bx(n-1)+b2x(n-2)+b3x(n-3)+bax(n-4) 22
22 FIR滤波器基本网络结构 按照H(z)或者差分方程式直接画出结构图如图 6.3.1所示。它可以用抽头延迟线实现。设N=5 (即,4阶FIR滤波器),则: 按结构图可以直接写出: ( ) ( ) ( 1) ( 2) ( 3) ( 4) 0 1 2 3 4 y n = b x n + b x n − + b x n − + b x n − + b x n − 图 6.3.1 FIR 滤波器直接结构的信号流图

FIR滤波器基本网络结构 级联型 将H(z)进行因式分解,并将共轭成对的零 点放在一起,形成一个系数为实数的二 阶形式。这样级联型网络结构就是由 阶和二阶实系数因式构成的,其中的因 式都可用直接型实现。 例6.3.1设FIR网络系统函数H(z)如下式: H(z)=0.96+2z1+2.8z2+1.5z3 画出H(z)的直接型结构和级联型结构。 23
23 FIR滤波器基本网络结构 级联型 将H(z)进行因式分解,并将共轭成对的零 点放在一起,形成一个系数为实数的二 阶形式。这样级联型网络结构就是由一 阶和二阶实系数因式构成的,其中的因 式都可用直接型实现。 例6.3.1 设FIR网络系统函数H(z)如下式: 画出H(z)的直接型结构和级联型结构。 1 2 3 ( ) 0.96 2 2.8 1.5 − − − H z = + z + z + z
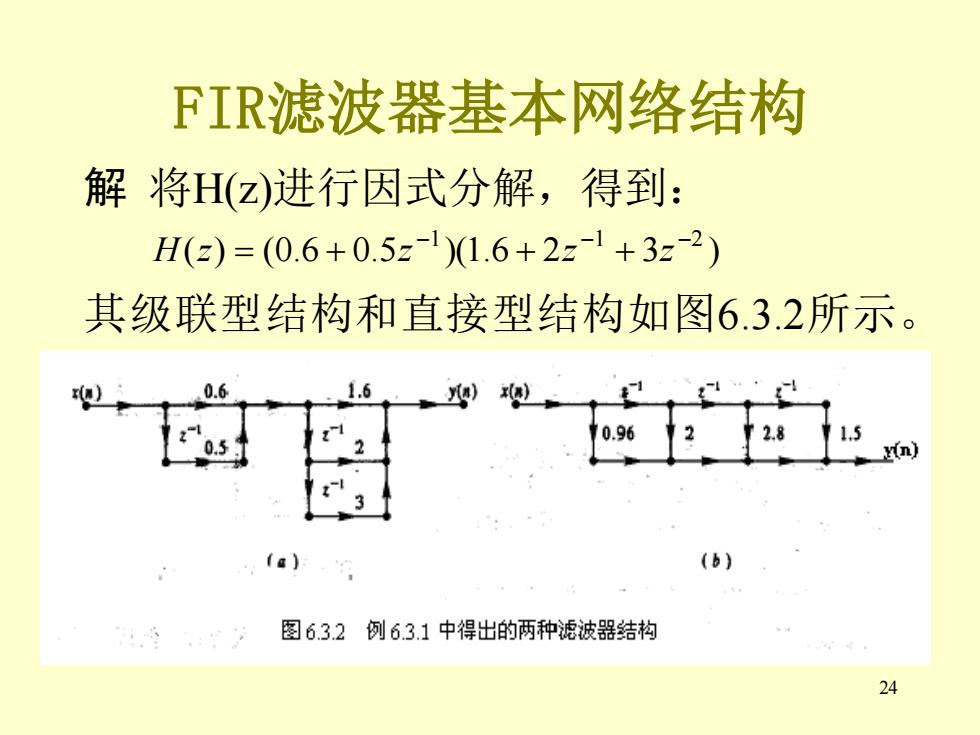
FIR滤波器基本网络结构 解将H(z)进行因式分解,得到: H(z)=(0.6+0.5z11.6+2z1+3z2) 其级联型结构和直接型结构如图6.3.2所示。 0.96 y(n) (a (b 图6.3.2例6.3.1中得出的两种滤波器结构 24
24 FIR滤波器基本网络结构 解 将H(z)进行因式分解,得到: 其级联型结构和直接型结构如图6.3.2所示。 ( ) (0.6 0.5 )(1.6 2 3 ) −1 −1 −2 H z = + z + z + z

FIR滤波器基本网络结构 当H(z)的阶次高于三阶时,可以用t2sos函数协助,它的 含义是由传递函数转换为二阶环节。其调用方法为 [sos,G]tf2sos(b,a) 其中:a,b为系统函数的分母、分子系数向量。 bor bu b21 1 au az SOS= boL bu b2 1 an azL 其每一行代表一个二阶环节的分子、分母系数。对第k行, 有 H4(日)=b4+iel+b2e2 1+a1k21+a2k22 25
25 FIR滤波器基本网络结构 当H(z)的阶次高于三阶时,可以用tf2sos函数协助,它的 含义是由传递函数转换为二阶环节。其调用方法为 [sos,G] = tf2sos(b,a) 其中:a,b为系统函数的分母、分子系数向量。 其每一行代表一个二阶环节的分子、分母系数。对第k行, 有 01 11 21 11 21 0L 1L 2L 1L 2L b b b 1 a a sos ... b b b 1 a a = , 2 2 1 1 2 2 1 0 1 1 ( ) − − − − + + + + = a z a z b b z b z H z k k k k k k